
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 (1)根据复合命题的真假判断进行判断.
(2)根据充分条件和必要条件的定义进行判断.
(3)根据函数解析式进行化简求解即可
(4)根据函数定义域的求法进行判断.
解答 解:(1)根据复合命题的真假关系可知,若p∨q为假命题,则p、q均为假命题,正确
(2)命题“?x∈[1,2),x2-a≤0”为真命题,
则a≥x2,
∵x∈[1,2),
∴x2∈[1,4),则a≥4,
则a≥1是命题为真命题的一个必要不充分条件,故(2)错误,
(3)已知函数$f({x-\frac{1}{x}})$=x2+$\frac{1}{x^2}$=(x-$\frac{1}{x}$)2+2,则f(x)=x2+2,
则f(2)=22+2=6;故(3)正确,
(4)若函数y=$\frac{mx-1}{{m{x^2}+4mx+3}}$的定义域为R,则等价为mx2+4mx+3≠0,
当m=0时,不等式mx2+4mx+3≠0,等价为3≠0,此时满足条件,故则实数m的取值范围是$({0,\frac{3}{4}})$错误.
故(1)(3)正确,
故选:C
点评 本题主要考查命题的真假判断,涉及复合命题,充分条件和必要条件,函数值的计算以及函数定义域问题,涉及的知识点较多,综合性较强,但难度不大.


 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | -6 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
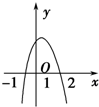
| A. | (-2,1) | B. | (0,3) | C. | (-1,2] | D. | (-∞,0)∪(3,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com