Question

10．已知点A（-1，0）以及抛物线y²=4x的焦点F，若P是抛物线上的动点，则$\frac{|PF|}{|PA|}$的取值范围是（　　）

• A． [0，$\frac{\sqrt{2}}{2}$]
• B． [$\frac{\sqrt{2}}{2}$，1]
• C． （$\frac{\sqrt{2}}{2}$，1]
• D． （$\frac{\sqrt{2}}{2}$，1）

Answer 1

分析 如图所示，由抛物线y²=4x，可得焦点F（1，0），抛物线的准线l：x=-1．设P（x₀，y₀），过点P作PM⊥l，垂足为M．可得|PF|=|PM|=x₀+1，|PA|=$\sqrt{|PM{|}^{2}+|AM{|}^{2}}$，可得$\frac{|PF{|}^{2}}{|PA{|}^{2}}$=$\frac{（{x}_{0}+1）^{2}}{（{x}_{0}+1）^{2}+4{x}_{0}}$，对x₀分类讨论，利用基本不等式的性质即可得出．

解答 解：如图所示，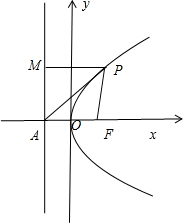
由抛物线y²=4x，可得焦点F（1，0），
抛物线的准线l：x=-1．
设P（x₀，y₀），过点P作PM⊥l，垂足为M．
则|PF|=|PM|=x₀+1，
|PA|=$\sqrt{|PM{|}^{2}+|AM{|}^{2}}$=$\sqrt{（{x}_{0}+1）^{2}+{y}_{0}^{2}}$=$\sqrt{（{x}_{0}+1）^{2}+4{x}_{0}}$，
∴$\frac{|PF{|}^{2}}{|PA{|}^{2}}$=$\frac{（{x}_{0}+1）^{2}}{（{x}_{0}+1）^{2}+4{x}_{0}}$，
当x₀=0时，$\frac{|PF{|}^{2}}{|PA{|}^{2}}$=$\frac{1}{1}$=1，即$\frac{|PF|}{|PA|}$=1．
当x₀≠0时，$\frac{|PF{|}^{2}}{|PA{|}^{2}}$=$\frac{1}{1+\frac{4{x}_{0}}{{x}_{0}^{2}+2{x}_{0}+1}}$=$\frac{1}{1+\frac{4}{{x}_{0}+\frac{1}{{x}_{0}}+2}}$$≥\frac{1}{1+\frac{4}{2\sqrt{{x}_{0}•\frac{1}{{x}_{0}}}+2}}$=$\frac{1}{2}$，当且仅当x₀=1时取等号．
即$\frac{|PF|}{|PA|}$≥$\frac{\sqrt{2}}{2}$．
综上可得：$\frac{\sqrt{2}}{2}$≤$\frac{|PF|}{|PA|}$≤1．
故选：B．

点评 本题考查了抛物线的定义标准方程及其性质、勾股定理、基本不等式的性质，考查了变形能力，考查了推理能力与计算能力，属于中档题．