
���� ��ֱ��l�IJ������̴���ԲO����ͨ���̣��ɵ�${t^2}+4\sqrt{3}t=0$�������ҳ�|AB|=|t1-t2|���ɵó���
��� �⣺ԲO�IJ�������Ϊ$\left\{\begin{array}{l}x=4cos��\\ y=4sin��\end{array}\right.$����Ϊ����������Ϊ��ͨ���̣�x2+y2=16��
��ֱ��l�IJ������̴���ԲO����ͨ���̣��ɵ�${t^2}+4\sqrt{3}t=0$��
���t1=0��${t_2}=-4\sqrt{3}$��
���ҳ�$|{AB}|=|{{t_1}-{t_2}}|=4\sqrt{3}$��
���� ���⿼���˲������̻�Ϊ��ͨ���̡�ֱ�߲������̵�Ӧ�ã�������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������P-ABC�У���PAB�͡�CAB������ABΪб�ߵĵ���ֱ�������Σ�
��ͼ��������P-ABC�У���PAB�͡�CAB������ABΪб�ߵĵ���ֱ�������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
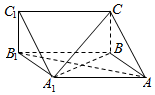 ��ͼ����������ABC-A1B1C1�У�A1A=AB��CB��A1ABB1��
��ͼ����������ABC-A1B1C1�У�A1A=AB��CB��A1ABB1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com