
分析 利用三角形的内角和以及两角和的正切函数,求解角C的正切值,然后求解角的大小,利用同角三角函数基本关系式,求出B的正弦函数值,然后利用正弦定理通过AB=$\sqrt{2}$,即可求AC.
解答 解:(1)∵A+B+C=π,
∴tanC=-tan(A+B)
∵tanA=2,tanB=3,
tan(A+B)=$\frac{tanA+tanB}{1-tanAtanB}$=$\frac{2+3}{1-6}$=-1,
∴tanC=1,
∵C是三角形的内角.
∴C=$\frac{π}{4}$,
∵tanB=3,可得:sinB=3cosB,
而sin2B+cos2B=1,且B为锐角,可求得sinB=$\frac{3\sqrt{10}}{10}$.
所以在△ABC中,由正弦定理得,AC=$\frac{AB}{sinC}$×sinB=$\frac{3\sqrt{10}}{5}$.
故答案为:$\frac{3\sqrt{10}}{5}$.
点评 本小题主要考查两角和的正切公式,以及同角三角函数的应用,并借助正弦定理考查边角关系的运算,对考生的化归与转化能力有较高要求,属于中档题.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{1}{2})$ | B. | $(\frac{1}{2},0)$ | C. | (0,1) | D. | (1,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
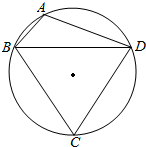 某城市在进行规划时,准备设计一个圆形的开放式公园,为达到社会和经济效益双丰收,园林公司进行如下设计,安排圆内接四边形ABCD作为绿化区域,其余作为市民活动区域,其中△ABD区域种植花木后出售,△BCD区域种植草皮后出售,已知草皮每平方米售价为a元,花木每平方米的售价是草皮每平方米售价的三倍,若BC=6km,AD=CD=4km.
某城市在进行规划时,准备设计一个圆形的开放式公园,为达到社会和经济效益双丰收,园林公司进行如下设计,安排圆内接四边形ABCD作为绿化区域,其余作为市民活动区域,其中△ABD区域种植花木后出售,△BCD区域种植草皮后出售,已知草皮每平方米售价为a元,花木每平方米的售价是草皮每平方米售价的三倍,若BC=6km,AD=CD=4km.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
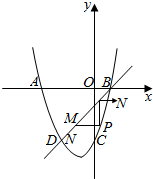 如图,抛物线y=ax2+2x-6与X轴交于点A(-6,0),B(点A在点B的左侧),与y轴交于点C,直线BD与抛物线交于点D,点D与点C关于该抛物线的对称轴对称.
如图,抛物线y=ax2+2x-6与X轴交于点A(-6,0),B(点A在点B的左侧),与y轴交于点C,直线BD与抛物线交于点D,点D与点C关于该抛物线的对称轴对称.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com