
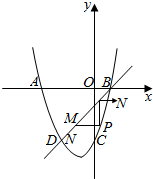
 如图,抛物线y=ax2+2x-6与X轴交于点A(-6,0),B(点A在点B的左侧),与y轴交于点C,直线BD与抛物线交于点D,点D与点C关于该抛物线的对称轴对称.
如图,抛物线y=ax2+2x-6与X轴交于点A(-6,0),B(点A在点B的左侧),与y轴交于点C,直线BD与抛物线交于点D,点D与点C关于该抛物线的对称轴对称.分析 (1)代入A的坐标,可得a的值;分别求得B,C,求得对称轴,可得D的坐标,求得CD的长;
(2)求出直线BD的方程,设出P的坐标,求得M,N的坐标,可得PM,PN的长,运用面积公式可得三角形PMN的面积,再由二次函数的最值的求法,可得最大值及此时P的坐标.
解答 解:(1)由A(-6,0),可得36a-12-6=0,
解得a=$\frac{1}{2}$,即有y=$\frac{1}{2}$x2+2x-6,
由y=0,可得x=-6或2,
即有B(2,0),C(0,-6),
抛物线的对称轴为x=-2,
即有D(-4,-6),则CD的长度为4;
(2)直线BD的斜率为k=$\frac{0+6}{2+4}$=1,
直线BD的方程为y=x-2,
可令P(m,$\frac{1}{2}$m2+2m-6),-4<m<2,
将x=m代入直线BD方程可得y=m-2,
即有|PN|=|$\frac{1}{2}$m2+m-4|,
将y=$\frac{1}{2}$m2+2m-6代入直线BD的方程可得x=$\frac{1}{2}$m2+2m-4,
即有|PM|=|$\frac{1}{2}$m2+m-4|,
则△MPN的面积为S=$\frac{1}{2}$|PM|2=$\frac{1}{2}$($\frac{1}{2}$m2+m-4)2
=$\frac{1}{2}$[$\frac{1}{2}$(m+1)2-$\frac{9}{2}$]2,-4<m<2,
当m=-1时,S=$\frac{81}{8}$,当m=-4或2时,S=0.
即有m=-1时,面积取得最大值,且为$\frac{81}{8}$.
此时P的坐标为(-1,-$\frac{15}{2}$).
点评 本题考查二次函数的解析式的求法,注意运用代入法,考查三角形的面积的最值的求法,注意运用直线方程和二次函数的最值求法,考查运算求解能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{3}$ 或 $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(2)<f(-$\frac{3}{2}$)<f(-1) | B. | f(-$\frac{3}{2}$)<f(-1)<f(2) | C. | f(2)<f(-1)<f(-$\frac{3}{2}$) | D. | f(2)<f(-$\frac{3}{2}$)<f(-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③④ | B. | ①②④ | C. | ①④ | D. | ①③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com