
分析 设A(x0,0)(x0>0),则直线l的方程为y=x-x0,设出直线方程,设直线l与椭圆相交于P(x1,y1),Q(x2,y2)两点,借助于韦达定理,从而可求得x0的值
解答 解:设A(x0,0)(x0>0),则直线l的方程为y=x-x0,
设直线l与椭圆相交于P(x1,y1),Q(x2,y2)两点,
由y=x-x0可得3x2-4x0x+2x02-12=0,
由根与系数的关系,有x1+x2=$\frac{4{x}_{0}}{3}$,x1x2=$\frac{{2x}_{0}^{2}-12}{3}$,
则|x1-x2|=$\sqrt{{{({x_1}+{x_2})}^2}-4{x_1}{x_2}}$=$\sqrt{\frac{16x_0^2}{9}-\frac{8x_0^2-48}{3}}=\frac{2}{3}\sqrt{36-2x_0^2}$.
所以$\frac{{4\sqrt{14}}}{3}=\sqrt{1+{k^2}}•|{x_1}-{x_2}|$,
即$\frac{{4\sqrt{14}}}{3}$=$\sqrt{2}•\frac{2}{3}$•$\sqrt{36-2x_0^2}$.
所以$x_0^2=4$.
又x0>0,所以x0=2,
所以A(2,0).
点评 本题考查直线与圆锥曲线的位置关系与弦长问题,难点在于弦长公式的灵活应用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A∩a=∅ | B. | a⊆A | C. | a∉A | D. | a∈A |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,使得${3^{x_0}}≤0$ | |
| B. | ?x∈R+,lgx>0 | |
| C. | “$x=\frac{π}{6}$”是“$cosx=\frac{{\sqrt{3}}}{2}$”的必要不充分条件 | |
| D. | “x=1”是“x≥1”的充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
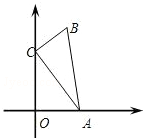 如图,在△ABC中,∠ACB=90°,AC=2,BC=1,点A、C分别在x轴、y轴上,当点A在x轴上运动时,点C随之在y轴上运动,在运动过程中,点B到原点O的最大距离是1+$\sqrt{2}$.
如图,在△ABC中,∠ACB=90°,AC=2,BC=1,点A、C分别在x轴、y轴上,当点A在x轴上运动时,点C随之在y轴上运动,在运动过程中,点B到原点O的最大距离是1+$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com