
如图,在△ABC中,B=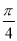 ,AC=2
,AC=2 ,cosC=
,cosC= .
.

(1)求sin∠BAC的值;
(2)设BC的中点为D,求中线AD的长.
科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-1数列的概念与简单表示法(解析版) 题型:选择题
在正项数列{an}中,若a1=1,且对所有n∈N*满足nan+1-(n+1)an=0,则a2014=( )
A.1011 B.1012 C.2013 D.2014
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:4-2平面向量的基本定理及坐标表示(解析版) 题型:解答题
已知点O(0,0)、A(1,2)、B(4,5)及 =
= +t
+t ,试问:
,试问:
(1)t为何值时,P在x轴上?在y轴上?P在第三象限?
(2)四边形OABP能否成为平行四边形?若能,求出相应的t值;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:4-1向量的概念及运算(解析版) 题型:选择题
对于向量a、b、c和实数λ,下列命题中真命题是( )
A.若a·b=0,则a=0或b=0
B.若λa=0,则λ=0或a=0
C.若a2=b2,则a=b或a=-b
D.若a·b=a·c,则b=c
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-8解三角形应用举例(解析版) 题型:填空题
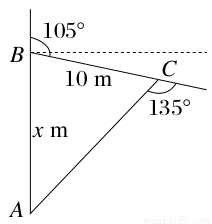
如图,在日本地震灾区的搜救现场,一条搜救狗从A处沿正北方向行进x m到达B处发现一个生命迹象,然后向右转105°,行进10 m到达C处发现另一生命迹象,这时它向右转135°后继续前行回到出发点,那么x=________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-7正弦定理和余弦定理(解析版) 题型:填空题
如图,在△ABC中,D是边AC上的点,且AB=AD,2AB= BD,BC=2BD,则sinC的值为________.
BD,BC=2BD,则sinC的值为________.

查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-6简单的三角恒等变换(解析版) 题型:选择题
在斜三角形ABC中,sinA=-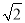 cosB·cosC,且tanB·tanC=1-
cosB·cosC,且tanB·tanC=1-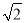 ,则角A的值为( )
,则角A的值为( )
A. B.
B.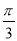 C.
C.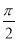 D.
D.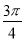
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-4正弦型函数的图象及应用(解析版) 题型:选择题
已知函数y=Asin(ωx+φ)+k的最大值是4,最小值是0,最小正周期是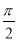 ,直线x=
,直线x=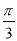 是其图象的一条对称轴,则下面各式中符合条件的解析式是( )
是其图象的一条对称轴,则下面各式中符合条件的解析式是( )
A.y=4sin(4x+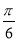 ) B.y=2sin(2x+
) B.y=2sin(2x+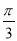 )+2
)+2
C.y=2sin(4x+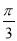 )+2 D.y=2sin(4x+
)+2 D.y=2sin(4x+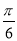 )+2
)+2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com