
【题目】已知圆![]() ,线段
,线段![]() 、
、![]() 都是圆
都是圆![]() 的弦,且
的弦,且![]() 与
与![]() 垂直且相交于坐标原点
垂直且相交于坐标原点![]() ,如图所示,设△
,如图所示,设△![]() 的面积为
的面积为![]() ,设△
,设△![]() 的面积为
的面积为![]() .
.
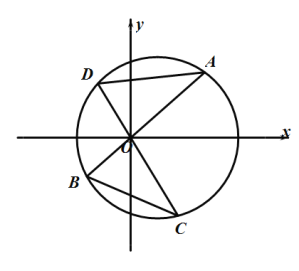
(1)设点![]() 的横坐标为
的横坐标为![]() ,用
,用![]() 表示
表示![]() ;
;
(2)求证:![]() 为定值;
为定值;
(3)用![]() 、
、![]() 、
、![]() 、
、![]() 表示出
表示出![]() ,试研究
,试研究![]() 是否有最小值,如果有,求出最小值,并写出此时直线
是否有最小值,如果有,求出最小值,并写出此时直线![]() 的方程;若没有最小值,请说明理由.
的方程;若没有最小值,请说明理由.
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:
【题目】已知各项均为正数的数列{an}的前n项和Sn满足S1>1,且![]() (nN*).
(nN*).
(1)求{an}的通项公式;
(2)设数列![]() 满足
满足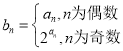 ,Tn为数列{bn}的前n项和,求Tn;
,Tn为数列{bn}的前n项和,求Tn;
(3)设![]() *(
*(![]() 为正整数),问是否存在正整数
为正整数),问是否存在正整数![]() ,使得当任意正整数n>N时恒有Cn>2015成立?若存在,请求出正整数
,使得当任意正整数n>N时恒有Cn>2015成立?若存在,请求出正整数![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】教材曾有介绍:圆![]() 上的点
上的点![]() 处的切线方程为
处的切线方程为![]() 。我们将其结论推广:椭圆
。我们将其结论推广:椭圆![]() 上的点
上的点![]() 处的切线方程为
处的切线方程为![]() ,在解本题时可以直接应用。已知,直线
,在解本题时可以直接应用。已知,直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点.
有且只有一个公共点.
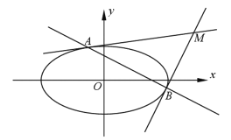
(1)求![]() 的值;
的值;
(2)设![]() 为坐标原点,过椭圆
为坐标原点,过椭圆![]() 上的两点
上的两点![]() 、
、![]() 分别作该椭圆的两条切线
分别作该椭圆的两条切线![]() 、
、![]() ,且
,且![]() 与
与![]() 交于点
交于点![]() 。当
。当![]() 变化时,求
变化时,求![]() 面积的最大值;
面积的最大值;
(3)在(2)的条件下,经过点![]() 作直线
作直线![]() 与该椭圆
与该椭圆![]() 交于
交于![]() 、
、![]() 两点,在线段
两点,在线段![]() 上存在点
上存在点![]() ,使
,使![]() 成立,试问:点
成立,试问:点![]() 是否在直线
是否在直线![]() 上,请说明理由.
上,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() ,定义椭圆C的“相关圆”E为:
,定义椭圆C的“相关圆”E为:![]() .若抛物线
.若抛物线![]() 的焦点与椭圆C的右焦点重合,且椭圆C的短轴长与焦距相等.
的焦点与椭圆C的右焦点重合,且椭圆C的短轴长与焦距相等.
(1)求椭圆C及其“相关圆”E的方程;
(2)过“相关圆”E上任意一点P作其切线l,若l 与椭圆![]() 交于A,B两点,求证:
交于A,B两点,求证:![]() 为定值(
为定值(![]() 为坐标原点);
为坐标原点);
(3)在(2)的条件下,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() (
(![]() ).
).
(1)计算![]() ,
,![]() ,
,![]() ,
,![]() ,并求数列
,并求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足
满足![]() ,求证:数列
,求证:数列![]() 是等比数列;
是等比数列;
(3)由数列![]() 的项组成一个新数列
的项组成一个新数列![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,设
,设![]() 为数列
为数列![]() 的前
的前![]() 项和,试求
项和,试求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】部分与整体以某种相似的方式呈现称为分形,一个数学意义上分形的生成是基于一个不断迭代的方程式,即一种基于递归的反馈系统.分形几何学不仅让人们感悟到科学与艺木的融合,数学与艺术审美的统一,而且还有其深刻的科学方法论意义.如图,由波兰数学家谢尔宾斯基1915年提出的谢尔宾斯基三角形就属于-种分形,具体作法是取一个实心三角形,沿三角形的三边中点连线,将它分成4个小三角形,去掉中间的那一个小三角形后,对其余3个小三角形重复上述过程逐次得到各个图形.

若在图④中随机选取-点,则此点取自阴影部分的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点与短轴两端点构成一个面积为2的等腰直角三角形,
的右焦点与短轴两端点构成一个面积为2的等腰直角三角形,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 在椭圆
在椭圆![]() 上,点
上,点![]() 在直线
在直线![]() 上,且
上,且![]() ,求证:
,求证:![]() 为定值;
为定值;
(3)设点![]() 在椭圆
在椭圆![]() 上运动,
上运动,![]() ,且点
,且点![]() 到直线
到直线![]() 的距离为常数
的距离为常数![]() ,求动点
,求动点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:对于数列![]() ,如果存在常数
,如果存在常数![]() ,使对任意正整数
,使对任意正整数![]() ,总有
,总有![]() 成立,那么我们称数列
成立,那么我们称数列![]() 为“
为“![]() ﹣摆动数列”.
﹣摆动数列”.
(1)设![]() ,
,![]() ,
,![]() ,判断数列
,判断数列![]() 、
、![]() 是否为“
是否为“![]() ﹣摆动数列”,并说明理由;
﹣摆动数列”,并说明理由;
(2)已知“![]() ﹣摆动数列”
﹣摆动数列”![]() 满足:
满足:![]() ,
,![]() .求常数
.求常数![]() 的值;
的值;
(3)设![]() ,
,![]() ,且数列
,且数列![]() 的前
的前![]() 项和为
项和为![]() .求证:数列
.求证:数列![]() 是“
是“![]() ﹣摆动数列”,并求出常数
﹣摆动数列”,并求出常数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com