
 ,则xy=96;
,则xy=96;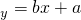 所表示的直线必恒经过点(1.5,2);
所表示的直线必恒经过点(1.5,2); ”的概率为
”的概率为 .
. ,“恰好一枚硬币正面朝上”的概率=
,“恰好一枚硬币正面朝上”的概率= .故①不正确;②由样本9,10,11,x,y的平均数是10,知x+y=20.由标准差是
.故①不正确;②由样本9,10,11,x,y的平均数是10,知x+y=20.由标准差是 ,知x2+y2-20(x+y)+200=8,所以xy=96.故②成立;③线性回归方程
,知x2+y2-20(x+y)+200=8,所以xy=96.故②成立;③线性回归方程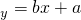 所表示的直线必恒经过点(1.5,5).故③不成立;④在AB上取M使
所表示的直线必恒经过点(1.5,5).故③不成立;④在AB上取M使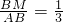 ,即
,即 ,过M作MN‖BC交AC于N,△ABC∽△AMN,由S在△ANM中不满足要求,S在梯形MNCB中满足要求,知概率=
,过M作MN‖BC交AC于N,△ABC∽△AMN,由S在△ANM中不满足要求,S在梯形MNCB中满足要求,知概率=
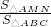 =
= .故④成立.
.故④成立.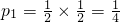 ,
,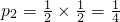 ,
, .故①不正确;
.故①不正确; ,
,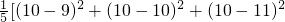 +(10-x)2+(10-y)2]=2,
+(10-x)2+(10-y)2]=2,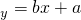 所表示的直线必恒经过点(1.5,5).故③不成立;
所表示的直线必恒经过点(1.5,5).故③不成立;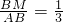 ,即
,即 ,
,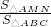 =
= =(
=( )2=
)2= ,
,
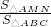 =
= .故④成立.
.故④成立.

 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com