
某超市从2014年甲、乙两种酸奶的日销售量(单位:箱)的数据中分别随机抽取100个,并按[0,10],(10,20],(20,30],(30,40],(40,50]分组,得到频率分布直方图如下:

假设甲、乙两种酸奶独立销售且日销售量相互独立.
(Ⅰ)写出频率分布直方图(甲)中的a的值;记甲种酸奶与乙种酸奶日销售量(单位:箱)的方差分别为 ,
, ,试比较
,试比较 与
与 的大小;(只需写出结论)
的大小;(只需写出结论)
(Ⅱ)估计在未来的某一天里,甲、乙两种酸奶的销售量恰有一个高于20箱且另一个不高于20箱的概率;
(Ⅲ)记X表示在未来3天内甲种酸奶的日销售量不高于20箱的天数,以日销售量落入各组的频率作为概率,求X的数学期望.
科目:高中数学 来源:2016届河北省高三上第二次月考文科数学试卷B(解析版) 题型:解答题
(本小题满分12分)若关于x的方程 有两个相等的实数根.
有两个相等的实数根.
(1)求实数a的取值范围.
(2)当a=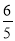 时,求
时,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年辽宁省高考前最后模拟理科数学试卷(解析版) 题型:选择题
已知椭圆
 (
( )的焦点为
)的焦点为 ,
, ,若点
,若点 在椭圆上,且满足
在椭圆上,且满足 (其中
(其中 为坐标原点),则称点
为坐标原点),则称点 为“
为“ ”点,则椭圆上的“
”点,则椭圆上的“ ”点有( )个
”点有( )个
A.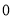 B.
B. C.
C.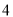 D.
D.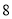
查看答案和解析>>
科目:高中数学 来源:2016届黑龙江省高三12月月考理科数学试卷(解析版) 题型:解答题
已知命题 :函数
:函数 在[-2,2]内有且仅有一个零点.命题
在[-2,2]内有且仅有一个零点.命题 :
: 在区间[
在区间[ ]内有解.若命题“
]内有解.若命题“ 且
且 ”是假命题,求实数
”是假命题,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年青海省高二期中考试数学试卷(解析版) 题型:解答题
在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面ABCD,
AE⊥BD,CB=CD=CF=1.

(1)求证:BD⊥平面AED;
(2)求B到平面FDC的距离.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江苏省无锡市四校高一上学期期中考试数学试卷(解析版) 题型:解答题
甲厂根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品 (百台),其总成本为
(百台),其总成本为 (万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本),销售收入
(万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本),销售收入 (万元)满足
(万元)满足 ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
(1)写出利润函数 的解析式(利润=销售收入-总成本);
的解析式(利润=销售收入-总成本);
(2)要使甲厂有盈利,求产量 的范围;
的范围;
(3)甲厂生产多少台产品时,可使盈利最多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com