练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．已知tan（θ-π）=2，则sin2θ+sinθcosθ-2cos2θ+1的值为$\frac{9}{5}$．

    分析 由条件利用诱导公式可得tanθ=2，再利用同角三角函数的基本关系把要求的式子化为正切函数的形式，从而求得结果．

    解答 解：∵已知tan（θ-π）=2=tanθ，则sin2θ+sinθcosθ-2cos2θ+1=$\frac{si{n}^{2}θ+sinθcosθ-2co{s}^{2}θ}{si{n}^{2}θ+co{s}^{2}θ}$+1=$\frac{ta{n}^{2}θ+tanθ-2}{ta{n}^{2}θ+1}$+1=$\frac{4+2-2}{4+1}$+1=$\frac{9}{5}$，
    故答案为：$\frac{9}{5}$．

    点评 本题主要考查同角三角函数的基本关系、诱导公式，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

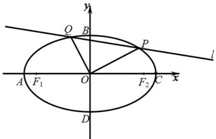    10．如图，在直角坐标系xOy中，椭圆$E：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的左右焦点分别为F1，F2，左、右、上、下四个顶点分别为A，C，B，D，四边形F1BF2D的面积与四边形ABCD的面积的比值为$\frac{{\sqrt{6}}}{3}$．
    （1）求椭圆E的离心率；
    （2）设椭圆E的焦距为$2\sqrt{2}$，直线l与椭圆E交于P，Q两点，且OP⊥OQ，求证：直线l恒与一定圆相切，并求出该圆的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．一个半径为2的球体经过切割后，剩余部分几何体的三视图如图所示，则该几何体的体积为8π．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．已知△ABC的内角A，B，C所对的边为a，b，c，A=60°，a=$\sqrt{13}$，b=1，则c=4，$\frac{a+b+c}{sinA+sinB+sinC}$=$\frac{2\sqrt{39}}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．设点P（x，y）在圆x2+（y-1）2=1上．
    （1）求$\sqrt{（x-2）^{2}+{y}^{2}}$的最小值；
    （2）求$\frac{y+2}{x+1}$的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知函数f（x）=$\left\{\begin{array}{l}{\frac{a}{x}，x＞2}\\{（x-1）^{3}，x≤2}\end{array}\right.$，a∈R．
    （1）当a=2时，求方程f（x）=x-1的实数解；
    （2）若方程f（x）=3x-1有且只有两个实数解，求实数a的取值范围；
    （3）已知函数g（x）=f（x）+2ax-1，其定义域为[2，4]，求函数的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知0＜α＜$\frac{π}{2}$，$\frac{π}{2}$＜β＜π，且cos（α+$\frac{π}{4}$）=$\frac{1}{3}$，cos（$\frac{π}{4}$-$\frac{β}{2}$）=$\frac{{\sqrt{3}}}{3}$，
    （1）求cosβ的值；            
    （2）求cos（2α+β）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．从5，6，7，8，9中任取两个不同的数，事件A=“取到的两个数之和为偶数”，事件B=“取到的两个数均为偶数”，则P（B|A）=（　　）
    A．$\frac{2}{5}$B．$\frac{1}{2}$C．$\frac{1}{4}$D．$\frac{1}{8}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．下列命题说法正确的是（　　）
    A．命题：“若x2+y2=1，则x=0且y=1”的否命题是：“若x2+y2≠1，则x≠0且y≠1”
    B．命题“?x∈R，x2+x-1＞0”的否定是“?x∈R，x2+x-1＜0”
    C．函数y=f（x+1）是偶函数，则f（x）的图象关于x=1对称
    D．向量$\overrightarrow a∥\overrightarrow b\;，\;\overrightarrow b∥\overrightarrow c$，则$\overrightarrow a∥\overrightarrow c$

    查看答案和解析>>

    同步练习册答案