考点:数列的函数特性
专题:等差数列与等比数列
分析:(1)只需举一反例即可;事实上设xn=1(n∈N*),易知数列xn是M数列,但Sn=n,|Sn+1-Sn|+|Sn-Sn-1|+…+|S2-S1|=n.由n的任意性知,数列Sn不是M数列.
(2)根据M数列的定义加以证明
(3)数列{an}都是M数列,则有|an+1-an|+|an-an-1|+…+|a2-a1|≤M1下面只需验证|an+12-an2|+|an2-an-12|+…+|a22-a12|≤M.
解答:
解:(1):若数列{xn}是M数列,则数列{xn}的前n项和{Sn}是M数列,此命题为假命题.
事实上设xn=1(n∈N*),易知数列xn是M数列,但Sn=n,
|Sn+1-Sn|+|Sn-Sn-1|+…+|S2-S1|=n.
由n的任意性知,数列Sn不是M数列.
(2):若数列{xn}的前n项和{Sn}是M数列,则数列{xn}不是M数列.此命题为真命题.
事实上,因为数列Sn是M数列,
所以存在正数M,对任意的n∈N*,
有|Sn+1-Sn|+|Sn-Sn-1|+…+|S2-S1|≤M,
即|xn+1|+|xn|+…+|x2|≤M.
于是|xn+1-xn|+|xn-xn-1|+…+|x2-x1|≤|xn+1|+2|xn|+2|xn-1|+…+2|x2|+|x1|≤2M+|x1|,
所以数列xn是M数列.
(3)若数列{an}是M数列,则数列{an2}也是M数列,此命题为真命题.
若数列是{an}M数列,则存在正数M,对任意的n∈N*有
|an+1-an|+|an-an-1|+…+|a2-a1|≤M
因为|an|=|an-an-1+an-1+an-2+…+a2-a1+a1|≤|an-an-1|+|an-1-an-2|+…+|a2-a1|+|a1|≤M+|a1|
记K=M+|a1|,则有|an+12-an2|=|(an+1+an)(an+1-an)
≤(|an+1|+|an|)|an+1-an|≤2K|an+1-an|
因此|an+12-an2|+|an2-an-12|+…+|a22-a12|≤2KM
故数列{an2}是M数列.
故答案为:②③
点评:考查学生理解数列概念,灵活运用数列表示法的能力,旨在考查学生的观察分析和归纳能力,特别是问题(2)(3)的设置,增加了题目的难度,同时也考查了等差数列的定义和分类讨论的思想,属难题.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案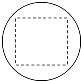 已知某一多面体内接于球构成一个组合体,如果该组合体的正视图,侧视图,俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是( )
已知某一多面体内接于球构成一个组合体,如果该组合体的正视图,侧视图,俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是( )