
分析 先求出函数的定义域,利用三角换元法,利用辅助角公式进行求解即可.
解答 解:由$\left\{\begin{array}{l}{12-2x≥0}\\{x-1≥0}\end{array}\right.$得$\left\{\begin{array}{l}{x≤6}\\{x≥1}\end{array}\right.$,即1≤x≤6,
即函数的定义域为[1,6].
y=$\sqrt{12-2x}$+$\sqrt{x-1}$=$\sqrt{2}$•$\sqrt{6-x}$+$\sqrt{x-1}$,
∵x-1+6-x=5,
∴令x-1=5sin2α,则6-x=5cos2α,α∈[0,$\frac{π}{2}$],
则y=$\sqrt{2}$•$\sqrt{5co{s}^{2}α}$+$\sqrt{5si{n}^{2}α}$=$\sqrt{10}$cosα+$\sqrt{5}$sinα,
=$\sqrt{15}$($\frac{\sqrt{10}}{\sqrt{15}}$cosα+$\frac{\sqrt{5}}{\sqrt{15}}$sinα)
=$\sqrt{15}$($\frac{\sqrt{6}}{3}$cosα+$\frac{\sqrt{3}}{3}$sinα),
令sinθ=$\frac{\sqrt{6}}{3}$,cosθ=$\frac{\sqrt{3}}{3}$,
则函数y=$\sqrt{15}$(sinθcosα+cosθsinα)=$\sqrt{15}$sin(α+θ)≤$\sqrt{15}$,
故函数的最大值为$\sqrt{15}$,
故答案为:$\sqrt{15}$.
点评 本题主要考查函数最值的求解,利用三角换元法,结合三角函数的辅助角公式是解决本题的关键.综合性较强,有一定的难度.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
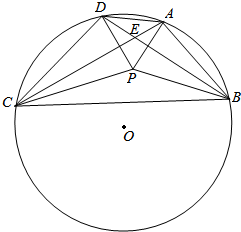 凸四边形ABCD的外接圆的圆心O,已知AC≠BD,AC与BD交于点E,若P为四边形ABCD内部一点,使得∠PAB+∠PCB=∠PBC+∠PDC=90°,求证:O,P,E三点共线.
凸四边形ABCD的外接圆的圆心O,已知AC≠BD,AC与BD交于点E,若P为四边形ABCD内部一点,使得∠PAB+∠PCB=∠PBC+∠PDC=90°,求证:O,P,E三点共线.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{5}{4}$,+∞) | B. | (1,$\frac{5}{4}$] | C. | [$\frac{7}{4}$,+∞) | D. | (1,$\frac{7}{4}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-3) | B. | (-3,-1) | C. | (-1,+∞) | D. | (0,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com