
【题目】已知函数![]() ,记
,记![]() 在点
在点![]() 处的切线为
处的切线为![]() .
.
(1)当![]() 时,求证:函数
时,求证:函数![]() 的图像(除切点外)均为切线
的图像(除切点外)均为切线![]() 的下方;
的下方;
(2)当![]() 时,求
时,求![]() 的最小值.
的最小值.
【答案】(1)见解析;(2)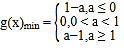
【解析】
(1)求得f(x)的导数,考虑极值点以及函数的凹凸性,即可得证;
(2)讨论a<0,a=0,a>1,a=1,0<a<1时,函数h(x)=f(x)﹣2lnx的导数和单调性,最值,即可得到所求g(x)的最小值.
(1)设切线方程为![]()
记![]()
![]() .
.
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() 在
在![]() 上单调递减.
上单调递减.
![]() ,
,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,
,![]() ,
,![]() 在
在![]() 上单调递减.
上单调递减.
∴![]() ,即
,即![]() ,当且仅当
,当且仅当![]() 时取“
时取“![]() ”.
”.
故命题成立
(2)![]() .
.
设![]() ,
,![]() ,
,
1)当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递减,且
上单调递减,且![]() .
.
∴![]() ,
,![]() 在
在![]() 上单调递增.
上单调递增.
∴![]()
2)当![]() 时,
时,![]() ,
,
设![]() ,
,![]() ,
,![]() 有两根
有两根![]() ,
,![]() ,
,
![]() ,
,![]() ,不妨令
,不妨令![]() ,
,
![]() ,
,![]() ,即
,即![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
![]() ,
,![]() ,即
,即![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
①当![]() ,即
,即![]() ,
,![]() ,
,![]() 在
在![]() 上单调递增.
上单调递增.
![]() ,∴
,∴![]() ;
;![]()
②当![]() ,即
,即![]() 时,
时,![]() ,
,
![]() ,
,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
![]() ,
,
![]() ,
,
存在![]() 使得
使得![]() ,
,
∴![]() .
.
综上可得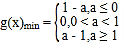 .
.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:高中数学 来源: 题型:
【题目】下列四个命题:
①函数![]() 是奇函数且在定义域上是单调递增函数;
是奇函数且在定义域上是单调递增函数;
②函数![]() 有两个零点,则
有两个零点,则![]() ;
;
③函数![]() ,则
,则![]() 的解集为
的解集为![]() ;
;
④函数![]() 的单调递减区间为
的单调递减区间为![]() .
.
其中正确命题的序号为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人同时各接受了600个零件的加工任务,甲比乙每分钟加工的数量多,两人同时开始加工,加工过程中甲因故障停止一会后又继续按原速加工,直到他们完成任务.如图表示甲比乙多加工的零件数量y(个)与加工时间x(分)之间的函数关系,A点横坐标为10,B点坐标为![]() ,C点横坐标为105.则甲每分钟加工的数量是_______,点D的坐标是_______.
,C点横坐标为105.则甲每分钟加工的数量是_______,点D的坐标是_______.
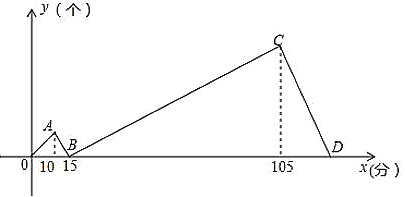
查看答案和解析>>
科目:高中数学 来源: 题型:
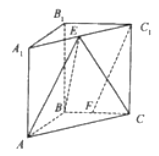
【题目】如图,在直角三棱柱![]() 中,
中,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,![]() ,
,![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)若直线![]() 和平面
和平面![]() 所成角的正弦值等于
所成角的正弦值等于![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 过点
过点![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)![]() ,
, ![]() 是过点
是过点![]() 且互相垂直的两条直线,其中
且互相垂直的两条直线,其中![]() 交圆
交圆![]() 于
于![]() ,
, ![]() 两点,
两点, ![]() 交椭圆
交椭圆![]() 于另一个点
于另一个点![]() ,求
,求![]() 面积取得最大值时直线
面积取得最大值时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行优惠促销活动,顾客仅可以从以下两种优惠方案中选择一种.
方案一:每满100元减20元;
方案二:满100元可抽奖一次.具体规则是从装有2个红球、2个白球的箱子随机取出3个球(逐个有放回地抽取),所得结果和享受的优惠如下表:(注:所有小球仅颜色有区别)
红球个数 | 3 | 2 | 1 | 0 |
实际付款 | 7折 | 8折 | 9折 | 原价 |
(1)该商场某顾客购物金额超过100元,若该顾客选择方案二,求该顾客获得7折或8折优惠的概率;
(2)若某顾客购物金额为180元,选择哪种方案更划算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com