
分析 (Ⅰ)求出点A极坐标,即可求点A的直角坐标,求出椭圆的直角坐标方程,即可求椭圆Γ的参数方程;
(Ⅱ)若E为椭圆Γ的下顶点,F为椭圆Γ上任意一点,求出向量的坐标,即可求$\overrightarrow{AE}•\overrightarrow{AF}$的最大值.
解答 解:(Ⅰ)射线$l:θ=\frac{π}{6}$与圆C:ρ=2交于点$A({2,\frac{π}{6}})$,
点A的直角坐标$({\sqrt{3},1})$;
椭圆Γ的方程为${ρ^2}=\frac{3}{{1+2{{sin}^2}θ}}$,直角坐标方程为$\frac{x^2}{3}+{y^2}=1$,
参数方程为$\left\{\begin{array}{l}x=\sqrt{3}cosθ\\ y=sinθ\end{array}\right.$(θ为参数);
(Ⅱ)设$F({\sqrt{3}cosθ,sinθ})$,∵E(0,-1),
∴$\overrightarrow{AE}=({-\sqrt{3},-2})$,$\overrightarrow{AF}=({\sqrt{3}cosθ-\sqrt{3},sinθ-1})$,∴$\overrightarrow{AE}•\overrightarrow{AF}=-3cosθ+3-2({sinθ-1})$
=$\sqrt{13}sin({θ+α})+5$,
当sin(θ+α)=1时,$\overrightarrow{AE}•\overrightarrow{AF}$的最大值为$\sqrt{13}+5$.
点评 本题考查三种方程的转化,考查向量知识的运用,属于中档题.


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
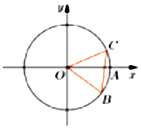 如图,圆O与x轴正半轴交点为A,点B,C在圆O上,圆C在第一象限,且B($\frac{4}{5}$,-$\frac{3}{5}$),∠AOC=α,BC=1,则cos($\frac{5π}{6}$-α)=-$\frac{3}{5}$.
如图,圆O与x轴正半轴交点为A,点B,C在圆O上,圆C在第一象限,且B($\frac{4}{5}$,-$\frac{3}{5}$),∠AOC=α,BC=1,则cos($\frac{5π}{6}$-α)=-$\frac{3}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 25 | 33 | m | 55 | 75 |
| A. | 46 | B. | 48 | C. | 50 | D. | 52 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②③④ | D. | ①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<b<a | B. | c<a<b | C. | a<b<c | D. | a<c<b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com