
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 首先,根据函数f(x)在定义域(0,+∞)上是单调函数,若对任意x∈(0,+∞),都有f[f(x)-$\frac{1}{x}$]=2,得到f(x)-$\frac{1}{x}$为一个常数,令f(x)-$\frac{1}{x}$=n,则f(n)=2,求出n,可求出函数的解析式,即可得出结论.
解答 解:根据题意,得若对任意x∈(0,+∞),都有f[f(x)-$\frac{1}{x}$]=2,得到f(x)-$\frac{1}{x}$为一个常数,
令f(x)-$\frac{1}{x}$=n,
则f(n)=2,
∴2-$\frac{1}{n}$=n,
∴n=1,
∴f(x)=1+$\frac{1}{x}$,
∴f($\frac{1}{6}$)=7,
故选:C.
点评 本题考查的知识点是函数的值,函数解析式的求法,其中抽象函数解析式的求法,要注意对已知条件及未知条件的凑配思想的应用.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直线 | B. | 圆 | C. | 线段 | D. | 射线 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
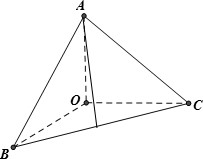 如图所示,在三棱锥A-OBC中,OA,OB,OC两两垂直且长度都为2,则这个三棱锥的体积为$\frac{4}{3}$;O到平面ABC的距离为$\frac{2\sqrt{3}}{3}$.
如图所示,在三棱锥A-OBC中,OA,OB,OC两两垂直且长度都为2,则这个三棱锥的体积为$\frac{4}{3}$;O到平面ABC的距离为$\frac{2\sqrt{3}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,n∥α,则m∥n | B. | 若m⊥α,n⊥α,则m∥n | ||
| C. | 若m∥α,n∥α,β∥α,则m∥n | D. | 若m∥n,m∥α,则n∥α |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 年产量/亩 | 年种植成本/亩 | 每吨售价 | |
| 黄瓜 | 4吨 | 1.2万元 | 0.55万元 |
| 韭菜 | 5吨 | 0.9万元 | 0.3万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x3 | B. | y=$\frac{1}{x-1}$ | C. | y=log2$\frac{1}{x}$ | D. | y=-tanx |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com