练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．在△ABC中，（a2+b2）sin（A-B）=（a2-b2）sin（A+B），其中a、b、c是内角A、B、C的对边，则△ABC的形状为等腰三角形或直角三角形．

    分析 利用两角和差的正弦函数公式化简，使用正弦定理即可得出A，B的关系，得出结论．

    解答 解：在△ABC中，∵（a2+b2）sin（A-B）=（a2-b2）sin（A+B），
    ∴（a2+b2）（sinAcosB-cosAsinB）=（a2-b2）（sinAcosB+cosAsinB），
    即sinAcosB•2b2=cosAsinB•2a2．
    所以sinAcosBsin2B=cosAsinBsin2A．
    sinBcosB=sinAcosA，即sin2B=sin2A．
    ∴2A=2B或2A+2B=180°，
    ∴A=B或A+B=90°，
    ∴三角形是等腰三角形或直角三角形．
    故答案为：等腰或直角三角形．

    点评 本题考查了正弦定理，三角函数的恒等变换，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    3．若β∈（0，π），则方程x2+y2sinβ=1所表示的曲线是（　　）
    A．圆B．椭圆C．双曲线D．椭圆或圆

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

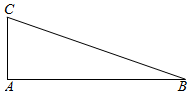    4．如图，在Rt△ABC中，∠CAB=90°，|AB|=2，|AC|=$\frac{\sqrt{2}}{2}$，一曲线E过点C，动点P在曲线E上运动，且保持|PA|+|PB|的值不变．
    （1）建立适当的坐标系，求曲线E的方程；
    （2）试根据（1）所求方程判断曲线是否为椭圆方程，若是，写出其长轴长、焦距、离心率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．△ABC的内角A，B，C所对的边分别为a，b，c．已知$\sqrt{3}$bcosA=asinB．
    （Ⅰ）求A；
    （Ⅱ）若a=$\sqrt{7}$，b=2，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知Sn是公差不为0的等差数列{an}的前n项和，且S1，S2，S4成等比数列，则$\frac{{a}_{2}+{a}_{5}}{{a}_{1}+{a}_{3}}$等于（　　）
    A．2B．4C．6D．8

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．等差数列{an}中，a5=3，a23=3a7
    （Ⅰ）求{an}的通项公式；
    （Ⅱ）设bn=$\frac{1}{{n{a_n}}}$，求数列{bn}}的前n项和{Sn}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知{an}是等差数列，其前n项和为Sn，{bn}为公比大于零的等比数列，若b1=a1=1，b2=5-a2，b3=S3-a3．
    （1）求数列{an}，{bn}的通项公式；
    （2）定义E（an）=$\frac{{{a_1}+{a_2}+…+{a_n}}}{n}$是数列{an}的前n项的数学期望，若E（bn）≥t-$\frac{1}{{E（{a_n}）}}$对任意的n∈N+恒成立，求实数t的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．曲线y=x•sinx在点M（π，0）处的切线方程是πx+y-π2=0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．设A={x|x2+mx+1=0}，若A∩{x|x＞0}=∅，求m取值范围．

    查看答案和解析>>

    同步练习册答案