
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于D.
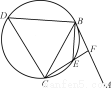
(1)证明:DB=DC;
(2)设圆的半径为1,BC=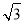 ,延长CE交AB于点F,求△BCF外接圆的半径.
,延长CE交AB于点F,求△BCF外接圆的半径.
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨选修4-4第2课时练习卷(解析版) 题型:解答题
若实数x、y、z满足x+2y+3z=a(a为常数),求x2+y2+z2的最小值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨选修4-2第1课时练习卷(解析版) 题型:解答题
已知矩阵M= ,N=
,N= ,矩阵MN对应的变换把曲线y=
,矩阵MN对应的变换把曲线y= sin
sin x变为曲线C,求曲线C的方程.
x变为曲线C,求曲线C的方程.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨选修4-2第1课时练习卷(解析版) 题型:解答题
求点A(2,0)在矩阵 对应的变换作用下得到的点的坐标.
对应的变换作用下得到的点的坐标.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨选修4-1第2课时练习卷(解析版) 题型:解答题
如图,在△ABC中,∠B=90°,以AB为直径的圆O交AC于D,过点D作圆O的切线交BC于E,AE交圆O于点F.求证:

(1)E是BC的中点;
(2)AD·AC=AE·AF.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨选修4-1第2课时练习卷(解析版) 题型:解答题
如图,已知P是圆O外一点,PD为圆O的切线,D为切点,割线PEF经过圆心O,若PF=12,PD=4 ,求圆O的半径长和∠EFD的大小.
,求圆O的半径长和∠EFD的大小.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨选修4-1第1课时练习卷(解析版) 题型:解答题
如图,在△ABC中,作直线DN平行于中线AM,设这条直线交边AB于点D,交边CA的延长线于点E,交边BC于点N.求证:AD∶AB=AE∶AC.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第十章第5课时练习卷(解析版) 题型:填空题
投掷两颗骰子,得到其向上的点数分别为m、n,设a=(m,n),则满足|a|<5的概率为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com