
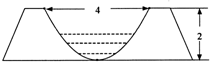
 Ϊ��Ӧ��ũ�彨�裬ij��ƻ������о�ˮ�����и��죬��֪��ˮ���ĺ������һ��������������Ϊˮ����ˣ���ͼ��������Ϊ4m������Ϊ2m��
Ϊ��Ӧ��ũ�彨�裬ij��ƻ������о�ˮ�����и��죬��֪��ˮ���ĺ������һ��������������Ϊˮ����ˣ���ͼ��������Ϊ4m������Ϊ2m������ ��1����������ϵ���������ߵķ���Ϊx2=2py��p��0��������֪��P��2��2�����������ϣ��Ƶ��������ߵķ��̣��ɵ�����APQB��������õ����ɵý��ۣ�
��2��Ϊ��ʹ�ڵ��������٣��������ε��������������������У����е�M��t��$\frac{1}{2}$t2����t��0�������ڵ�M�����߷���Ϊy-$\frac{1}{2}$t2=t��x-t�����ɴ����Ƶ�����Ƹ��ں��ˮ���ĵ�Ϊ$\sqrt{2}$mʱ����ʹ��Ȩ�����������������٣�
���  �⣺��1��������ͼ������ϵ��
�⣺��1��������ͼ������ϵ��
�������ߵķ���Ϊx2=2py��p��0����
����֪��P��2��2�����������ϣ���p=1��
�������ߵķ���Ϊx2=2y��
��A��t��$\frac{1}{2}$t2�������ʱ����APQB���ΪS��t��=$\frac{1}{2}$��2t+4����2-$\frac{1}{2}$t2����
��S�䣨t��=-$\frac{3}{2}{t}^{2}-2t+2=0$��t=$\frac{2}{3}$��
t�ʣ�0��$\frac{2}{3}$����S�䣨t����0��t�ʣ�$\frac{2}{3}$��2����S�䣨t����0
��t=$\frac{2}{3}$��Smax��t��=$\frac{128}{27}$��
����ˮ����Ϊ$\frac{4}{3}$mʱ�������������������٣�
��2��Ϊ��ʹ�ڵ��������٣��������ε��������������������У�
��ͼ��
���е�M��t��$\frac{1}{2}$t2����t��0��
�����ڵ�M�����߷���Ϊy-$\frac{1}{2}$t2=t��x-t����
��y=0��y=2����A��$\frac{1}{2}$t��0����B��$\frac{t}{2}+\frac{2}{t}$��2����
���ʱ����OABC�����ΪS��t��=$\frac{1}{2}$��t+$\frac{2}{t}$��•2=t+$\frac{2}{t}$��2$\sqrt{2}$��
���ҽ���t=$\sqrt{2}$ʱ���Ⱥų�����
��ʱ|OA|=$\frac{\sqrt{2}}{2}$��
����Ƹ��ں��ˮ���ĵ�Ϊ$\sqrt{2}$mʱ�����������٣�
���� ���⿼�麯�������������е�ʵ��Ӧ�ã�����ʱҪ�������⣬ע���ھ������е����������������ؽ��еȼ�ת����ע���֪ʶ����������ʽ�ĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 24�� | B�� | 30�� | C�� | 36�� | D�� | 48�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{Ƶ��}{��������}$ | B�� | ����Ƶ�� | C�� | Ƶ�� | D�� | $\frac{Ƶ��}{���}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com