

分析 根据条件可得出$\overrightarrow{DE}=\frac{3}{4}\overrightarrow{DC},\overrightarrow{AB}=\overrightarrow{DC}$,进而得到$\overrightarrow{AE}=\frac{3}{4}\overrightarrow{DC}-\overrightarrow{DA}$,代入$\overrightarrow{AB}•\overrightarrow{AE}$进行数量积的运算,便可求出该数量积的值.
解答 解:$\overrightarrow{DE}=3\overrightarrow{EC}$;
∴$\overrightarrow{DE}=\frac{3}{4}\overrightarrow{DC}$;
∴$\overrightarrow{AE}=\overrightarrow{DE}-\overrightarrow{DA}$=$\frac{3}{4}\overrightarrow{DC}-\overrightarrow{DA}$,且$\overrightarrow{AB}=\overrightarrow{DC}$;
∴$\overrightarrow{AB}•\overrightarrow{AE}=\overrightarrow{DC}•(\frac{3}{4}\overrightarrow{DC}-\overrightarrow{DA})$
=$\frac{3}{4}{\overrightarrow{DC}}^{2}-\overrightarrow{DC}•\overrightarrow{DA}$
=12-0
=12.
故答案为:12.
点评 考查向量数乘的几何意义,以及相等向量的概念,向量数量积的运算及计算公式.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{3π}{4}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
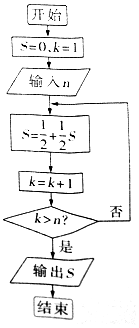 庄子说:“一尺之锤,日取其半,万世不竭”,这句话描述的是一个数列问题,现用程序框图描述,如图所示,若输入某个正整数n后,输出的S∈($\frac{15}{16}$,$\frac{63}{64}$),则输入的n的值为( )
庄子说:“一尺之锤,日取其半,万世不竭”,这句话描述的是一个数列问题,现用程序框图描述,如图所示,若输入某个正整数n后,输出的S∈($\frac{15}{16}$,$\frac{63}{64}$),则输入的n的值为( )| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
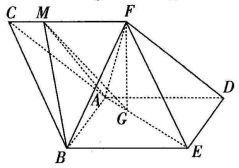 如图,三棱柱ABC-DEF中,侧面ABED是边长为2的菱形,且∠ABE=$\frac{π}{3}$,BC=$\frac{\sqrt{21}}{2}$,四棱锥F-ABED的体积为2,点F在平面ABED内的正投影为G,且G在AE上,点M是在线段CF上,且CM=$\frac{1}{4}$CF.
如图,三棱柱ABC-DEF中,侧面ABED是边长为2的菱形,且∠ABE=$\frac{π}{3}$,BC=$\frac{\sqrt{21}}{2}$,四棱锥F-ABED的体积为2,点F在平面ABED内的正投影为G,且G在AE上,点M是在线段CF上,且CM=$\frac{1}{4}$CF.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -$\frac{2}{3}$ | C. | -$\frac{12}{5}$ | D. | $\frac{\sqrt{2}-4}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -$\frac{5\sqrt{2}+1}{7}$ | C. | $\frac{1}{3}$ | D. | -$\frac{7}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com