
分析 (1)由等差数列{an}的公差为1,且a1,a3,a9成等比数列,可得${a}_{3}^{2}$=a1a9,即$({a}_{1}+2)^{2}$=a1(a1+8),解得a1.再利用等差数列的通项公式及其前n项和公式即可得出.
(2)$\frac{1}{{S}_{n}}$=$\frac{2}{n(n+1)}$=2$(\frac{1}{n}-\frac{1}{n+1})$,再利用“裂项求和”与数列的单调性即可得出.
解答 (1)解:∵等差数列{an}的公差为1,且a1,a3,a9成等比数列,
∴${a}_{3}^{2}$=a1a9,∴$({a}_{1}+2)^{2}$=a1(a1+8),解得a1=1.
∴an=1+(n-1)=n,
Sn=$\frac{n(n+1)}{2}$.
(2)证明:$\frac{1}{{S}_{n}}$=$\frac{2}{n(n+1)}$=2$(\frac{1}{n}-\frac{1}{n+1})$,
∴数列{$\frac{1}{{S}_{n}}$}的前n项和为Tn=2$[(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{n}-\frac{1}{n+1})]$=2$(1-\frac{1}{n+1})$<2.
∴Tn<2.
点评 本题考查了“裂项求和”、等比数列与等差数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
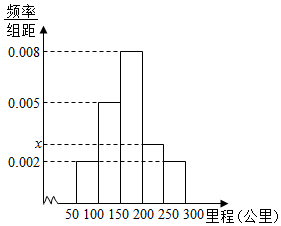 2015年1月1日新《环境保护法》实施后,2015年3月18日,交通运输部发布《关于加快推进新能源汽车在交通运输行业推广应用的实施意见》,意见指出,至2020年,新能源汽车在交通运输行业的应用初具规模,在城市公交、出租汽车和城市物流配送等领域的总量达到30万辆;新能源汽车配套服务设施基本完备,新能源汽车运营效率和安全水平明显提升.随着新能源汽车的迅速发展,关于新能源汽车是纯电动汽车的续航里程(单次充电后能行驶的最大里程)一直是消费者最为关注的话题.
2015年1月1日新《环境保护法》实施后,2015年3月18日,交通运输部发布《关于加快推进新能源汽车在交通运输行业推广应用的实施意见》,意见指出,至2020年,新能源汽车在交通运输行业的应用初具规模,在城市公交、出租汽车和城市物流配送等领域的总量达到30万辆;新能源汽车配套服务设施基本完备,新能源汽车运营效率和安全水平明显提升.随着新能源汽车的迅速发展,关于新能源汽车是纯电动汽车的续航里程(单次充电后能行驶的最大里程)一直是消费者最为关注的话题.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{e}$ | B. | 1 | C. | e | D. | e2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
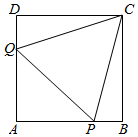 某地政府为提升城市形象,在该地区边长为1的正方形ABCD的空地建文化广场,在正方形ABCD的内部规划一块△CPQ区域种植花草,并满足P,Q分别为边AB,DA上的动点,且∠PCQ=$\frac{π}{3}$,问∠PCB多大时才能使△CPQ面积的最小,并求出最小值.
某地政府为提升城市形象,在该地区边长为1的正方形ABCD的空地建文化广场,在正方形ABCD的内部规划一块△CPQ区域种植花草,并满足P,Q分别为边AB,DA上的动点,且∠PCQ=$\frac{π}{3}$,问∠PCB多大时才能使△CPQ面积的最小,并求出最小值.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com