
| A. | 0 个 | B. | 1 个 | C. | 2 个 | D. | 3 个 |
分析 设点A(x,y)(x<0)在f(x)的图象上,则点B(-x,-y)也在f(x)的图象上,
$\left\{\begin{array}{l}{y={x}^{2}+2x}\\{-y=\frac{-x+1}{e}}\end{array}\right.$⇒ex2+(2e-1)x+1=0,令g(x)=ex2+(2e-1)x+1,判定方程ex2+(2e-1)x+1=0负实根个数即可.
解答 解:设点A(x,y)(x<0)在f(x)的图象上,则点B(-x,-y)也在f(x)的图象上,
$\left\{\begin{array}{l}{y={x}^{2}+2x}\\{-y=\frac{-x+1}{e}}\end{array}\right.$⇒ex2+(2e-1)x+1=0,令g(x)=ex2+(2e-1)x+1,二次函数g(x)的对称轴x=$\frac{2e-1}{-2e}<0$,g(0)=1>0,△=(2e-1)2-4e>0,
∴方程ex2+(2e-1)x+1=0有两个负实根,故函数 f (x)=$\left\{\begin{array}{l}{{x}^{2}+2x,x<0}\\{\frac{x+1}{e},x≥0}\end{array}\right.$,则 f (x) 的“姊妹点对”有2个.
故选:B.
点评 本题考查了学生对新定义的接受能力及导数的综合应用,同时考查了零点个数的判断,属于中档题


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案科目:高中数学 来源:2016-2017学年河北正定中学高二上月考一数学(理)试卷(解析版) 题型:解答题
已知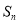 为等比数列
为等比数列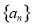 的前
的前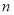 项和,且
项和,且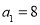 ,
,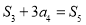 .
.
(1)求数列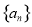 的通项公式;
的通项公式;
(2)若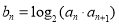 ,
,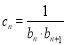 ,记数列
,记数列 与
与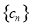 的前
的前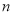 项和分别为
项和分别为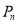 ,
,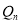 ,求
,求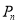 与
与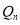 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 50 | B. | 100 | C. | 150 | D. | 200 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
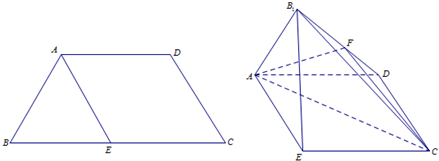
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 成绩(单位:分) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 数学 | 8 | 12 | 40 | 32 | 8 |
| 物理 | 7 | 18 | 40 | 29 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com