
 在一个几何体的三视图中,正视图与俯视图如右图所示,则相应的侧视图可以为( )
在一个几何体的三视图中,正视图与俯视图如右图所示,则相应的侧视图可以为( )| A. |  | B. |  | C. |  | D. |  |
 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源:2016-2017学年河北正定中学高二上月考一数学(文)试卷(解析版) 题型:选择题
若不等式 表示的平面区域为
表示的平面区域为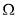 ,
,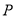 、
、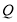 均为
均为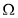 内一点,
内一点,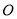 为坐标原点,
为坐标原点, ,则下列判断正确的是( )
,则下列判断正确的是( )
A.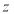 的最小值为
的最小值为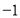 B.
B.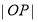 的最小值为
的最小值为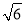
C.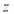 的最大值为
的最大值为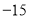 D.
D.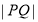 的最大值为
的最大值为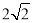
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 流量x | 0≤x<5 | 5≤x<10 | 10≤x<15 | 15≤x<20 | 20≤x<25 | x≥25 |
| 频率 | 0.05 | 0.25 | 0.30 | 0.25 | 0.15 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
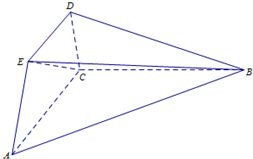 如图,已知平面ABC⊥平面ACDE,且△ABC为等腰直角三角形,AC=BC=4,等腰梯形ACDE中,AC∥DE且AE=DE=2.
如图,已知平面ABC⊥平面ACDE,且△ABC为等腰直角三角形,AC=BC=4,等腰梯形ACDE中,AC∥DE且AE=DE=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 个 | B. | 1 个 | C. | 2 个 | D. | 3 个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com