
°Њћвƒњ°њќ™ѕм”¶ ЃЊ≈іу±®Єжћб≥цµƒ µ ©ѕзіе’с–Ћ’љ¬‘£ђƒ≥іе„ѓЌґ„ ![]() Ќт‘™љ®∆рЅЋ“ї„щ¬ћ…Ђ≈©≤ъ∆ЈЉ”є§≥І.Њ≠”™÷–£ђµЏ“їƒк÷І≥ц
Ќт‘™љ®∆рЅЋ“ї„щ¬ћ…Ђ≈©≤ъ∆ЈЉ”є§≥І.Њ≠”™÷–£ђµЏ“їƒк÷І≥ц![]() Ќт‘™£ђ“‘Їу√њƒкµƒ÷І≥ц±»…ѕ“їƒк‘цЉ”ЅЋ
Ќт‘™£ђ“‘Їу√њƒкµƒ÷І≥ц±»…ѕ“їƒк‘цЉ”ЅЋ![]() Ќт‘™£ђі”µЏ“їƒк∆р√њƒк≈©≥°∆Јѕъ џ ’»лќ™
Ќт‘™£ђі”µЏ“їƒк∆р√њƒк≈©≥°∆Јѕъ џ ’»лќ™![]() Ќт‘™£®«∞
Ќт‘™£®«∞![]() ƒкµƒіњјы»у„џЇѕ=«∞
ƒкµƒіњјы»у„џЇѕ=«∞![]() ƒкµƒ „№ ’»л-«∞
ƒкµƒ „№ ’»л-«∞![]() ƒкµƒ„№÷І≥ц-Ќґ„ ґо
ƒкµƒ„№÷І≥ц-Ќґ„ ґо![]() Ќт‘™£©.
Ќт‘™£©.
£®1£©Є√≥Іі”µЏЉЄƒкњ™ Љ”ѓјы£њ
£®2£©Є√≥ІµЏЉЄƒкƒк∆љЊщіњјы»уіпµљ„оіу£њ≤Ґ«у≥цƒк∆љЊщіњјы»уµƒ„оіу÷µ.
°Њір∞Є°њ(1) і”µЏ![]() њ™ Љ”ѓјы(2) Є√≥ІµЏ
њ™ Љ”ѓјы(2) Є√≥ІµЏ![]() ƒкƒк∆љЊщіњјы»уіпµљ„оіу£ђƒк∆љЊщіњјы»у„оіу÷µќ™
ƒкƒк∆љЊщіњјы»уіпµљ„оіу£ђƒк∆љЊщіњјы»у„оіу÷µќ™![]() Ќт‘™
Ќт‘™
°Њљвќц°њ ‘ћвЈ÷ќц£Ї(1)ЄщЊЁєЂ љµ√µљ![]() £ђЅоЇѓ э÷µіу”Џ0љвµ√≤ќ эЈґќІ£ї£®2£©ЄщЊЁєЂ љµ√µљ
£ђЅоЇѓ э÷µіу”Џ0љвµ√≤ќ эЈґќІ£ї£®2£©ЄщЊЁєЂ љµ√µљ![]() £ђ”…Њщ÷µ≤їµ» љµ√µљЇѓ э„о÷µ.
£ђ”…Њщ÷µ≤їµ» љµ√µљЇѓ э„о÷µ.
љвќц£Ї
”…ћв“вњ…÷™«∞![]() ƒкµƒіњјы»у„№ЇЌ
ƒкµƒіњјы»у„№ЇЌ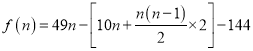
![]()
£®1£©”…![]() £ђЉі
£ђЉі![]() £ђљвµ√
£ђљвµ√![]()
”…![]() ÷™£ђі”µЏ
÷™£ђі”µЏ![]() њ™ Љ”ѓјы.
њ™ Љ”ѓјы.
£®2£©ƒк∆љЊщіњјы»у![]()
“тќ™![]() £ђЉі
£ђЉі![]()
Ћщ“‘![]()
µ±«“љцµ±![]() £ђЉі
£ђЉі![]() ±µ»Ї≈≥…ЅҐ.
±µ»Ї≈≥…ЅҐ.
ƒк∆љЊщіњјы»у„оіу÷µќ™![]() Ќт‘™£ђ
Ќт‘™£ђ
є Є√≥ІµЏ![]() ƒкƒк∆љЊщіњјы»уіпµљ„оіу£ђƒк∆љЊщіњјы»у„оіу÷µќ™
ƒкƒк∆љЊщіњјы»уіпµљ„оіу£ђƒк∆љЊщіњјы»у„оіу÷µќ™![]() Ќт‘™.
Ќт‘™.
°Њћв–Ќ°њљвірћв
°Њљб ш°њ
21
°Њћвƒњ°њ“—÷™ эЅ–![]() µƒ«∞
µƒ«∞![]() ѕоЇЌќ™
ѕоЇЌќ™![]() £ђ≤Ґ«“¬ъ„г
£ђ≤Ґ«“¬ъ„г![]() £ђ
£ђ ![]() .
.
£®1£©«у эЅ–![]() Ќ®ѕоєЂ љ£ї
Ќ®ѕоєЂ љ£ї
£®2£©…и![]() ќ™ эЅ–
ќ™ эЅ–![]() µƒ«∞
µƒ«∞![]() ѕоЇЌ£ђ«у÷§£Ї
ѕоЇЌ£ђ«у÷§£Ї ![]() .
.

| ƒкЉґ | Єя÷–њќ≥ћ | ƒкЉґ | ≥х÷–њќ≥ћ |
| Єя“ї | Єя“ї√вЈ—њќ≥ћЌ∆Љц£° | ≥х“ї | ≥х“ї√вЈ—њќ≥ћЌ∆Љц£° |
| Єяґю | Єяґю√вЈ—њќ≥ћЌ∆Љц£° | ≥хґю | ≥хґю√вЈ—њќ≥ћЌ∆Љц£° |
| Єя»э | Єя»э√вЈ—њќ≥ћЌ∆Љц£° | ≥х»э | ≥х»э√вЈ—њќ≥ћЌ∆Љц£° |
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ“—÷™Їѓ э![]() µƒµЉЇѓ эќ™
µƒµЉЇѓ эќ™![]() £ђ∆д÷–aќ™≥£ э
£ђ∆д÷–aќ™≥£ э
(I)ћ÷¬џf(x)µƒµ•µч–‘;
(Ґт)µ±a=-1 ±,»ф≤їµ» љ![]() Їг≥…ЅҐ,«у µ эmµƒ»°÷µЈґќІ
Їг≥…ЅҐ,«у µ эmµƒ»°÷µЈґќІ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ“—÷™Їѓ э![]()
(1)µ±![]() ±£ђ«уЇѓ э
±£ђ«уЇѓ э![]() µƒµ•µч‘ц«шЉд£ї
µƒµ•µч‘ц«шЉд£ї
(2)»ф«ъѕя![]() ‘Џµг
‘Џµг![]() і¶µƒ«–ѕя
і¶µƒ«–ѕя![]() ”л«ъѕя
”л«ъѕя![]() ”–«“÷ї”–“їЄцєЂє≤µг£ђ«у µ э
”–«“÷ї”–“їЄцєЂє≤µг£ђ«у µ э![]() µƒ»°÷µЈґќІ.
µƒ»°÷µЈґќІ.
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ‘Џ°чABC÷–£ђƒЏљ«A£ђB£ђCґ‘±яЈ÷±рќ™a£ђb£ђc£ђ«“c£Љa£ђ“—÷™ ![]() =©Б2£ђtanB=2
=©Б2£ђtanB=2 ![]() £ђb=3£Ѓ
£ђb=3£Ѓ
£®1£©«уaЇЌcµƒ÷µ£ї
£®2£©«уsin£®B©БC£©µƒ÷µ£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ…и![]() µƒƒЏљ«
µƒƒЏљ«![]() £ђ
£ђ ![]() £ђ
£ђ ![]() Ћщґ‘µƒ±яЈ÷±рќ™
Ћщґ‘µƒ±яЈ÷±рќ™![]() £ђ
£ђ ![]() £ђ
£ђ ![]() £ђ«“
£ђ«“![]() £ђ
£ђ ![]() .
.
£®1£©µ±![]() ±£ђ«у
±£ђ«у![]() µƒ÷µ£ї
µƒ÷µ£ї
£®2£©µ±![]() µƒ√жїэќ™
µƒ√жїэќ™![]() ±£ђ«у
±£ђ«у![]() µƒ÷№≥§.
µƒ÷№≥§.
°Њір∞Є°њ(1) ![]() (2)8
(2)8
°Њљвќц°њ ‘ћвЈ÷ќц£Ї£®1£©”…![]() £ђ
£ђ ![]() £ђ”…’эѕ“ґ®јнµ√µљ
£ђ”…’эѕ“ґ®јнµ√µљ![]() £ї£®2£©ЄщЊЁ√жїэєЂ љµ√µљ
£ї£®2£©ЄщЊЁ√жїэєЂ љµ√µљ![]() £ђ‘ў”…”аѕ“ґ®јнµ√µљ
£ђ‘ў”…”аѕ“ґ®јнµ√µљ![]() £ђљшґшµ√µљ
£ђљшґшµ√µљ![]() .
.
љвќц£Ї
£®1£©“тќ™![]() £ђЋщ“‘
£ђЋщ“‘![]()
”…’эѕ“ґ®јн![]() £ђњ…µ√
£ђњ…µ√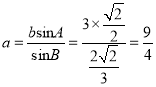
£®2£©“тќ™![]() µƒ√жїэ
µƒ√жїэ![]()
Ћщ“‘![]()
”…”аѕ“ґ®јн![]()
µ√![]() £ђЉі
£ђЉі![]()
Ћщ“‘![]() £ђ
£ђ
Ћщ“‘![]()
Ћщ“‘£ђ ![]() µƒ÷№≥§ќ™
µƒ÷№≥§ќ™![]()
°Њћв–Ќ°њљвірћв
°Њљб ш°њ
18
°Њћвƒњ°њ»зЌЉ£ђ‘ЏЋƒјв„ґ![]() ÷–£ђµ„√ж
÷–£ђµ„√ж![]() «∆љ––Ћƒ±я–ќ£ђ
«∆љ––Ћƒ±я–ќ£ђ ![]() £ђ
£ђ ![]() £ђ
£ђ ![]() £ђ
£ђ ![]() µ„√ж
µ„√ж![]() .
.
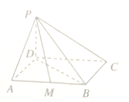
£®1£©«у÷§£Ї ![]() ∆љ√ж
∆љ√ж![]() £ї
£ї
£®2£©»ф![]() ќ™
ќ™![]() µƒ÷–µг£ђ«у÷±ѕя
µƒ÷–µг£ђ«у÷±ѕя![]() ”л∆љ√ж
”л∆љ√ж![]() Ћщ≥…љ«µƒ’эѕ“÷µ.
Ћщ≥…љ«µƒ’эѕ“÷µ.
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ‘Џ»зЌЉЋщ ЊµƒЉЄЇќће÷–£ђЋƒ±я–ќ![]() ќ™’эЈљ–ќ£ђЋƒ±я–ќ
ќ™’эЈљ–ќ£ђЋƒ±я–ќ![]() ќ™÷±љ«ћЁ–ќ£ђ
ќ™÷±љ«ћЁ–ќ£ђ ![]() £ђ
£ђ ![]() £Ѓ
£Ѓ
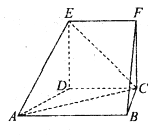
£®1£©«у![]() ”л∆љ√ж
”л∆љ√ж![]() Ћщ≥…љ«µƒ’эѕ“÷µ£ї
Ћщ≥…љ«µƒ’эѕ“÷µ£ї
£®2£©ѕяґќ![]() їт∆д—”≥§ѕя…ѕ «Јсіж‘Џµг
їт∆д—”≥§ѕя…ѕ «Јсіж‘Џµг![]() £ђ є∆љ√ж
£ђ є∆љ√ж![]() ∆љ√ж
∆љ√ж![]() £њ÷§√чƒгµƒљб¬џ£Ѓ
£њ÷§√чƒгµƒљб¬џ£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ“—÷™ЉѓЇѕA£љ{x|3°№![]() °№27}£ђB£љ{x|
°№27}£ђB£љ{x|![]() >1}£Ѓ
>1}£Ѓ
(1)Ј÷±р«уA°…B£ђ(![]() )°»A£ї
)°»A£ї
(2)“—÷™ЉѓЇѕC£љ{x|1<x<a}£ђ»фCA£ђ«у µ эaµƒ»°÷µЈґќІ£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ“—÷™≈„ќпѕя![]() µƒґ•µг‘Џ„ш±к‘≠µг£ђљєµг‘Џ
µƒґ•µг‘Џ„ш±к‘≠µг£ђљєµг‘Џ![]() ÷б…ѕ£ђ«“єэµг
÷б…ѕ£ђ«“єэµг![]() .
.
£®I£©«у![]() µƒ±к„ЉЈљ≥ћ£ї
µƒ±к„ЉЈљ≥ћ£ї
£®Ґт£©»ф![]() ќ™„ш±к‘≠µг£ђ
ќ™„ш±к‘≠µг£ђ ![]() «
«![]() µƒљєµг£ђєэµг
µƒљєµг£ђєэµг![]() «“«г–±љ«ќ™
«“«г–±љ«ќ™![]() µƒ÷±ѕя
µƒ÷±ѕя![]() љї
љї![]() ”Џ
”Џ![]() £ђ
£ђ ![]() Ѕљµг£ђ«у
Ѕљµг£ђ«у![]() µƒ√жїэ.
µƒ√жїэ.
≤йњіір∞ЄЇЌљвќц>>
єъЉ —І–£”≈—° - ЅЈѕ∞≤бЅ–±н - ‘ћвЅ–±н
Їю±± °ї•Ѕ™Ќшќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®∆љћ® | Ќш…ѕ”–Ї¶–≈ѕҐЊў±®„®«ш | µз–≈’©∆≠Њў±®„®«ш | …жјъ Ј–йќё÷ч“е”–Ї¶–≈ѕҐЊў±®„®«ш | …ж∆у«÷»®Њў±®„®«ш
ќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®µзї∞£Ї027-86699610 Њў±®” ѕд£Ї58377363@163.com