
【题目】已知集合A={x|3≤![]() ≤27},B={x|
≤27},B={x|![]() >1}.
>1}.
(1)分别求A∩B,(![]() )∪A;
)∪A;
(2)已知集合C={x|1<x<a},若CA,求实数a的取值范围.
【答案】(1)A∩B={x|2<x≤3},(CRB)∪A={x|x≤3};(2)a的取值范围是(﹣∞,3]
【解析】
试题分析:(1)解指数不等式我们可以求出集合A,解对数不等式,我们可以求集合B,再由集合补集的运算规则,求出CRB,进而由集合交集和并集的运算法则,即可求出A∩B,(CRB)∪A;
(2)由(1)中集合A,结合集合C={x|1<x<a},我们分C=和C≠两种情况,分别求出对应的实数a的取值,最后综合讨论结果,即可得到答案.
解:(1)A={x|3≤3x≤27}={x|1≤x≤3}
B={x|log2x>1}={x|x>2}
A∩B={x|2<x≤3}
(CRB)∪A={x|x≤2}∪{x|1≤x≤3}={x|x≤3}
(2)当a≤1时,C=![]() ,
,
此时CA
当a>1时,
CA,则1<a≤3
综上所述,a的取值范围是(﹣∞,3]


科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1(α>b>0)的右焦点到直线x﹣y+3
=1(α>b>0)的右焦点到直线x﹣y+3 ![]() =0的距离为5,且椭圆的一个长轴端点与一个短轴端点间的距离为
=0的距离为5,且椭圆的一个长轴端点与一个短轴端点间的距离为 ![]() .
.
(1)求椭圆C的方程;
(2)在x轴上是否存在点Q,使得过Q的直线与椭圆C交于A、B两点,且满足 ![]() +
+ ![]() 为定值?若存在,请求出定值,并求出点Q的坐标;若不存在,请说明理由.
为定值?若存在,请求出定值,并求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应十九大报告提出的实施乡村振兴战略,某村庄投资![]() 万元建起了一座绿色农产品加工厂.经营中,第一年支出
万元建起了一座绿色农产品加工厂.经营中,第一年支出![]() 万元,以后每年的支出比上一年增加了
万元,以后每年的支出比上一年增加了![]() 万元,从第一年起每年农场品销售收入为
万元,从第一年起每年农场品销售收入为![]() 万元(前
万元(前![]() 年的纯利润综合=前
年的纯利润综合=前![]() 年的 总收入-前
年的 总收入-前![]() 年的总支出-投资额
年的总支出-投资额![]() 万元).
万元).
(1)该厂从第几年开始盈利?
(2)该厂第几年年平均纯利润达到最大?并求出年平均纯利润的最大值.
【答案】(1) 从第![]() 开始盈利(2) 该厂第
开始盈利(2) 该厂第![]() 年年平均纯利润达到最大,年平均纯利润最大值为
年年平均纯利润达到最大,年平均纯利润最大值为![]() 万元
万元
【解析】试题分析:(1)根据公式得到![]() ,令函数值大于0解得参数范围;(2)根据公式得到
,令函数值大于0解得参数范围;(2)根据公式得到![]() ,由均值不等式得到函数最值.
,由均值不等式得到函数最值.
解析:
由题意可知前![]() 年的纯利润总和
年的纯利润总和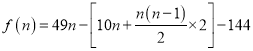
![]()
(1)由![]() ,即
,即![]() ,解得
,解得![]()
由![]() 知,从第
知,从第![]() 开始盈利.
开始盈利.
(2)年平均纯利润![]()
因为![]() ,即
,即![]()
所以![]()
当且仅当![]() ,即
,即![]() 时等号成立.
时等号成立.
年平均纯利润最大值为![]() 万元,
万元,
故该厂第![]() 年年平均纯利润达到最大,年平均纯利润最大值为
年年平均纯利润达到最大,年平均纯利润最大值为![]() 万元.
万元.
【题型】解答题
【结束】
21
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,并且满足
,并且满足![]() ,
, ![]() .
.
(1)求数列![]() 通项公式;
通项公式;
(2)设![]() 为数列
为数列![]() 的前
的前![]() 项和,求证:
项和,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x3+ax2+bx+c满足f'(0)=4,f'(-2)=0。
(1)求a,b的值及曲线y=f(x)在点(0,f(0))处的切线方程;
(2)若函数f(x)有三个不同的零点,求c的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC为锐角三角形,命题p:不等式logcosC ![]() >0恒成立,命题q:不等式logcosC
>0恒成立,命题q:不等式logcosC ![]() >0恒成立,则复合命题p∨q、p∧q、¬p中,真命题的个数为( )
>0恒成立,则复合命题p∨q、p∧q、¬p中,真命题的个数为( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定长为2的线段AB的两个端点在以点(0, ![]() )为焦点的抛物线x2=2py上移动,记线段AB的中点为M,求点M到x轴的最短距离,并求此时点M的坐标。
)为焦点的抛物线x2=2py上移动,记线段AB的中点为M,求点M到x轴的最短距离,并求此时点M的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com