
����Ŀ��������Ժ����ͬ�⣬֣�ݳɹ���Χ�������ij��У�ijУѧ������ԡ�֣�ݵķ�չ��������20��ѧ�������ʾ������֣�����100�֣����õ���ͼ1��ʾ��Ҷͼ�� 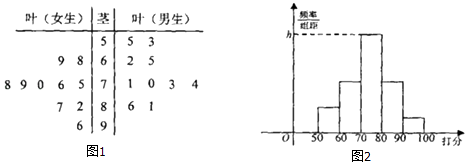
���ֱ��������Ů����ֵ�ƽ���֣�������ѧ����������Ů����ֵ����ݷֲ������
������ͼ2���մ������[0��60����[60��70����[70��80����[80��90����[90��100]���Ƶ�ֱ��ͼ�У�����߾��εĸߣ�
���Ӵ����70�����£�����70�֣���ͬѧ�г�ȡ3�ˣ�����Ů�������еĸ��ʣ�
���𰸡��⣺����Ů����ֵ�ƽ����Ϊ��
![]() =
= ![]() ��68+69+75+76+70+79+78+82+87+96��=78��
��68+69+75+76+70+79+78+82+87+96��=78��
������ֵ�ƽ����Ϊ��
![]() =
= ![]() ��55+53+62+65+71+70+73+74+86+81��=69��
��55+53+62+65+71+70+73+74+86+81��=69��
�Ӿ�Ҷͼ������Ů�������Լ��У����������Է�ɢ��
����20��ѧ���У��������[0��60����[60��70����[70��80����[80��90����[90��100]�е�ѧ�����ֱ�Ϊ��
2�ˣ�4�ˣ�9�ˣ�4�ˣ�1�ˣ�
�������[70��80����������࣬��9�ˣ�����Ƶ��Ϊ�� ![]() =0.45��
=0.45��
����߾��εĸ�h= ![]() =0.045��
=0.045��
�������70�����£�����70�֣���ͬѧ��6�ˣ���������4�ˣ�Ů��2�ˣ�
���г�ȡ3�ˣ������¼�����n= ![]() =20��
=20��
��Ů�������еĶ����¼��dz��е�3��ͬѧ����������
����Ů�������еĸ���p=1�� ![]() =1��
=1�� ![]() =
= ![]() ��
��
���������������þ�Ҷͼ�����Ů����ֵ�ƽ���ֺ�������ֵ�ƽ���֣��Ӿ�Ҷͼ������Ů�������Լ��У����������Է�ɢ��
����20��ѧ���У��������[0��60����[60��70����[70��80����[80��90����[90��100]�е�ѧ�����ֱ�Ϊ��2�ˣ�4�ˣ�9�ˣ�4�ˣ�1�ˣ��������[70��80����������࣬��9�ˣ�����Ƶ��Ϊ0.45���ɴ��������߾��εĸߣ�
�������70�����£�����70�֣���ͬѧ��6�ˣ���������4�ˣ�Ů��2�ˣ���Ů�������еĶ����¼��dz��е�3��ͬѧ�����������ɴ����ö����¼����ʼ��㹫ʽ�������Ů�������еĸ��ʣ�
�����㾫����ͨ���������Ƶ�ʷֲ�ֱ��ͼ�;�Ҷͼ������Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ���Ƕ���ͬ���ݵ����ֲ�ͬ���﷽ʽ.�ý��յı���ı����ݵ����з�ʽ������ʽ����չʾ���ݵķֲ����.ͨ����ͼ�ȿ��Դ���������ȡ��Ϣ���ֿ�������ͼ�δ�����Ϣ����Ҷͼ�ֳơ�֦Ҷͼ��������˼·�ǽ������е�����λ�����бȽϣ������Ĵ�С���������仯�����λ��Ϊһ�����ɣ����������仯���λ������Ϊ��֦��Ҷ�����������ɵĺ��棬�����Ϳ�������ؿ���ÿ�����ɺ���ļ�������ÿ���������Ƕ��ټ����Խ����⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=aexlnx+ ![]() ������y=f��x���ڵ㣨1��f��1�����������߷���Ϊy=e��x��1��+2��
������y=f��x���ڵ㣨1��f��1�����������߷���Ϊy=e��x��1��+2��
������a��b��
����֤����f��x����1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ص�ӰԺΪ���˽��Ӱ�ԶԿ�Ҫ��ӳ��һ����Ӱ��Ʊ�۵Ŀ�����������һ�ε��У��õ���Ʊ��x(��λ��Ԫ)�������Ӱ����y(��λ������)�Ľ�����±���
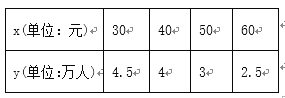
(1)������ϱ��ṩ�����ݣ�����С���˷����y����x�����Իع鷽�̣�
(2)����(1)����������Իع鷽�̣���Ʊ�۶�Ϊ70Ԫ��Ԥ��õ�ӰԺ������Ӱ�����������ع�ֱ�ߵ�б�ʺͽؾ����С���˷����ƹ�ʽ�ֱ�Ϊ��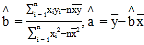
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�Ȳ�����{an}��ǰn��n��N*�����ΪSn �� a3=3���Ҧ�Sn=anan+1 �� �ڵȱ�����{bn}�У�b1=2�ˣ�b3=a15+1�� ����������{an}��{bn}��ͨ�ʽ��
����������{cn}��ǰn��n��N*�����ΪTn �� �� ![]() ����Tn ��
����Tn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ԲC��x2+y2=4��ֱ��l��y=x����ԲC����ȡһ��A��ֱ��l�ľ���С��1�ĸ���Ϊ�� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����DΪ����ʽ��  ����ʾ��ƽ������B��a��b��Ϊ��һ������һ�㣬����������D�ڵ���һ��A��x��y������
����ʾ��ƽ������B��a��b��Ϊ��һ������һ�㣬����������D�ڵ���һ��A��x��y������ ![]() ��������a+b�����ֵ���ڣ� ��
��������a+b�����ֵ���ڣ� ��
A.0
B.1
C.2
D.3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=2 ![]() ��AD=
��AD= ![]() ��MΪDC���е㣬����DAM��AM�۵���D��AM��λ�ã�AD���BM��
��MΪDC���е㣬����DAM��AM�۵���D��AM��λ�ã�AD���BM�� 
��1����֤��ƽ��D��AM��ƽ��ABCM��
��2����EΪD��B���е㣬������E��AM��D�������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ϊx2+y2��4x��2y+4=0����OΪ���㣬x��������Ϊ���Ὠ��������ϵ��
��1����l����ͨ������C�ļ����귽�̣�
��2����֪l��C����P��Q����|PQ|��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com