
分析 解法一:求出导函数,通过f′(x)<0的解为(a,a+4),利用子集关系,转化求解即可.
解法二:求出f′(x),通过f′(x)≤0在区间(-1,2)上恒成立,利用二次函数的性质求解即可.
解答 解法一:f′(x)=x2-2(a+2)x+a(a+4)=(x-a)(x-a-4),…(4分)
f′(x)<0的解为(a,a+4),…(7分)
∵f(x)在区间(-1,2)内单调递减,
∴(-1,2)⊆(a,a+4),…(10分)
由此得a≤-1且a+4≥2,a的范围是[-2,-1].…(12分)
解法二:f′(x)=x2-2(a+2)x+a(a+4),…(2分)
∵f(x)在区间(-1,2)内单调递减,
∴f′(x)≤0在区间(-1,2)上恒成立,…(4分)
∵二次函数f′(x)=x2-2(a+2)x+a(a+4)的开口向上,
∴f′(-1)=a2+6a+5≤0且f′(2)=a2-4≤0 …(10分)
解得a的范围是[-2,-1].…(12分)
点评 本题考查函数的导数的应用,函数恒成立,函数的单调性单调区间的求法,转化思想的应用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 产量每增加1000件,单位成本下降2.13元 | |
| B. | 产量每减少1000件,单位成本下降2.13元 | |
| C. | 产量每增加1000件,单位成本上升2130元 | |
| D. | 产量每减少1000件,单位成本上升2130元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 分析法 | B. | 反证法 | C. | 综合法 | D. | 间接证明法 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1≤x≤4} | B. | {x|2<x≤3} | C. | {x|2≤x<3} | D. | {x|-1<x<4} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
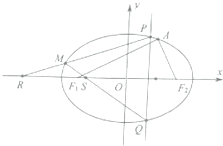 如图,已知椭圆C:$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{{b}^{2}}=1(0<b<3)$的左、右焦点分别为F1、F2,椭圆上存在一点A,使得AF1=2AF2,且∠F1AF2=90°
如图,已知椭圆C:$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{{b}^{2}}=1(0<b<3)$的左、右焦点分别为F1、F2,椭圆上存在一点A,使得AF1=2AF2,且∠F1AF2=90°查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<a<b | B. | b<c<a | C. | a<c<b | D. | c<b<a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com