Question

9．某城市为配合国家“一带一路”战略，发展城市旅游经济，拟在景观河道的两侧，沿河岸直线l₁与l₂修建景观（桥），如图所示，河道为东西方向，现要在矩形区域ABCD内沿直线将l₁与l₂接通．
已知AB=60m，BC=80m，河道两侧的景观道路修复费用为每米1万元，架设在河道上方的景观桥EF部分的修建费用为每米2万元．

（1）若景观桥长120m时，求桥与河道所成角的大小；
（2）如何设计景观桥EF的位置，使矩形区域ABCD内的总修建费用最低？最低总造价是多少？

Answer 1

分析 （1）过E作BC的垂线，利用三角函数的定义计算夹角；
（2）用河道与桥梁的夹角α表示出公路两侧的长度及公路间的长度，得到建造费用关于α的函数关系式，使用换元法判断函数的单调性得出最小值．

解答 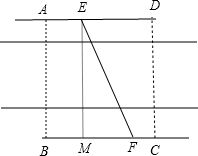解：（1）过E作FM⊥BC，则EM=AB=60，EF=120，
∴sin∠EFM=$\frac{EM}{EF}=\frac{1}{2}$，
∴∠EFM=$\frac{π}{6}$，即桥与河道所成角为$\frac{π}{6}$．
（2）设桥与河道的夹角为α（tanα≥$\frac{3}{4}$），
则MF=$\frac{60}{tanα}$，EF=$\sqrt{3600+\frac{3600}{ta{n}^{2}α}}$=60$\sqrt{1+\frac{1}{ta{n}^{2}α}}$，
∴AE+FC=80-MF=80-$\frac{60}{tanα}$，
设总修建费用为y万元，则y=80-$\frac{60}{tanα}$+120$\sqrt{1+\frac{1}{ta{n}^{2}α}}$，
令$\frac{1}{tanα}$=x，（0＜x≤$\frac{4}{3}$）则y=80-60x+120$\sqrt{1+{x}^{2}}$，
y′=-60+$\frac{120x}{\sqrt{1+{x}^{2}}}$，令y′=0得x=$\frac{\sqrt{3}}{3}$，
当0＜x$＜\frac{\sqrt{3}}{3}$时，y′＜0，当$\frac{\sqrt{3}}{3}＜x＜\frac{4}{3}$时，y′＞0，
∴当x=$\frac{\sqrt{3}}{3}$，y取得最小值80+60$\sqrt{3}$．
当x=$\frac{\sqrt{3}}{3}$时，tanα=$\sqrt{3}$，α=60°．
当桥与河道时夹角为60°时，建造费用最小，最小费用为80+60$\sqrt{3}$万元．

点评 本题考查了函数模型的选择及应用，考查了利用导数求闭区间上的最值，把费用正确表示为角α的函数关系是解答该题的关键，是中档题．