
分析 (Ⅰ)由题设得:$2{S_n}={n^2}-n$,所以$2{S_{n-1}}={({n-1})^2}-n-1$(n≥2),可得an=Sn-Sn-1(n≥2).当n=1时,a1=S1=0,利用等差数列的通项公式即可得出.
(II)利用裂项求和方法即可得出.
解答 解:(Ⅰ)由题设得:$2{S_n}={n^2}-n$,所以$2{S_{n-1}}={({n-1})^2}-n-1$(n≥2)
所以an=Sn-Sn-1=n-1(n≥2)
当n=1时,a1=S1=0,数列{an}是a1=0为首项、公差为1的等差数列
故an=n-1.
(Ⅱ)由(Ⅰ)知:${b_n}=\left\{\begin{array}{l}\frac{1}{{\sqrt{{a_{n+1}}}+\sqrt{{a_{n+3}}}}},n=2k-1\\ \frac{n+1}{{a_{n+1}^2•a_{n+3}^2}},n=2k\end{array}\right.$
=$\left\{\begin{array}{l}\frac{{\sqrt{n+2}-\sqrt{n}}}{2},n=2k-1\\ \frac{1}{4}({\frac{1}{n^2}-\frac{1}{{{{({n+2})}^2}}}}),n=2k\end{array}\right.$.
T2n=b1+b2+b3+…+b2n=$\frac{1}{2}({\sqrt{3}-1+\sqrt{5}}\right.$$-\sqrt{3}+\sqrt{7}-\sqrt{5}…$$\left.{+\sqrt{n+2}-\sqrt{n}})$$+\frac{1}{4}[{({\frac{1}{2^2}-\frac{1}{4^2}})+({\frac{1}{4^2}-\frac{1}{6^2}})}\right.$$+({\frac{1}{6^2}-\frac{1}{8^2}})+…$$\left.{+({\frac{1}{n^2}-\frac{1}{{{{({n+2})}^2}}}})}]$
=$\frac{{\sqrt{n+2}-1}}{2}+\frac{1}{16}$$-\frac{1}{{4{{({n+2})}^2}}}$.
点评 本题考查了等差数列的通项公式与求和公式、裂项求和方法,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
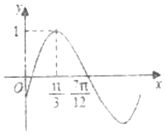 函数f(x)=Asin(ωx+φ)(A>0,ω>0,$|φ|<\frac{π}{2}$)的图象如图所示,为了得到g(x)=Asinωx的图象,可以将f(x)的图象( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,$|φ|<\frac{π}{2}$)的图象如图所示,为了得到g(x)=Asinωx的图象,可以将f(x)的图象( )| A. | 向左平移$\frac{π}{12}$个单位长度 | B. | 向右平移$\frac{π}{12}$个单位长度 | ||
| C. | 向左平移$\frac{π}{6}$个单位长度 | D. | 向右平移$\frac{π}{6}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 第十届中国艺术节在山东济南胜利闭幕,山东省京剧院的京剧《瑞蚨祥》获得“第十四届文华奖--文华大奖”,评委给她的9个得分去掉1个最高分,去掉1个最低分,7个剩余分数的平均分为91,现场做的9个分数的茎叶图后来有一个数据模糊,无法辨认,在图中以x表示:则7个剩余分数的方差为$\frac{36}{7}$.
第十届中国艺术节在山东济南胜利闭幕,山东省京剧院的京剧《瑞蚨祥》获得“第十四届文华奖--文华大奖”,评委给她的9个得分去掉1个最高分,去掉1个最低分,7个剩余分数的平均分为91,现场做的9个分数的茎叶图后来有一个数据模糊,无法辨认,在图中以x表示:则7个剩余分数的方差为$\frac{36}{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{1,\frac{5}{4}}]$ | B. | [-1,1] | C. | (-∞,1] | D. | $({-∞,\frac{5}{4}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com