
分析 (1)由题意求出抛物线的焦点坐标及准线方程,利用导数求出过抛物线上一点P(x0,$\frac{{x}_{0}^{2}}{2p}$)的切线的斜率k,写出切线方程,得到Q的坐标,进一步求出FQ的斜率,由kFQ×k=-1可得FQ⊥l;
(2)由(1)可设直线L的方程为y=$\frac{{x}_{0}}{p}x+b$,求得d,得到D=$\sqrt{{p}^{2}+{{x}_{0}}^{2}}$.再由点到直线的距离公式得D=$\frac{|-\frac{{p}^{2}}{2}+b|}{\sqrt{{{x}_{0}}^{2}+{p}^{2}}}$=$\sqrt{{p}^{2}+{{x}_{0}}^{2}}$,求出b,得到直线方程,与抛物线方程联立,设M(x1,y1),N(x2,y2),MN的中点为(x′,y′),利用根与系数的关系即可求得线段MN中点的轨迹方程.
解答 (1)证明:由题意可知:抛物线C:x2=2py的焦点F(0,$\frac{p}{2}$),准线为:y=-$\frac{p}{2}$,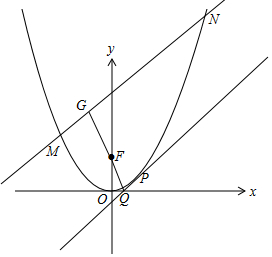
过抛物线上一点P(x0,$\frac{{x}_{0}^{2}}{2p}$),作抛物线的切线,
则切线的斜率k=$y′{丨}_{x={x}_{0}}$=$\frac{{x}_{0}}{p}$,
切线方程为:y-$\frac{{x}_{0}^{2}}{2p}$=$\frac{{x}_{0}}{p}$(x-x0),交x轴于Q($\frac{{x}_{0}}{2}$,0),
则直线FQ的斜率kFQ=$\frac{\frac{p}{2}-0}{0-\frac{{x}_{0}}{2}}$=-$\frac{p}{{x}_{0}}$,
∵kFQ×k=-1,∴FQ⊥l;
(2)解:由(1)可设直线L的方程为y=$\frac{{x}_{0}}{p}x+b$,
∵d=$\sqrt{(\frac{p}{2})^{2}+(\frac{{x}_{0}}{2})^{2}}=\frac{1}{2}\sqrt{{p}^{2}+{{x}_{0}}^{2}}$,∴D=$\sqrt{{p}^{2}+{{x}_{0}}^{2}}$.
由点到直线的距离公式得D=$\frac{|-\frac{{p}^{2}}{2}+b|}{\sqrt{{{x}_{0}}^{2}+{p}^{2}}}$=$\sqrt{{p}^{2}+{{x}_{0}}^{2}}$,
整理得:$|-\frac{{p}^{2}}{2}+b|={p}^{2}+{{x}_{0}}^{2}$,
∴$-\frac{{p}^{2}}{2}+b=±({p}^{2}+{{x}_{0}}^{2})$,则b=$\frac{3{p}^{2}}{2}+{{x}_{0}}^{2}$或b=$-\frac{{p}^{2}}{2}-{{x}_{0}}^{2}$(舍).
∴直线L的方程为$y=\frac{{x}_{0}}{p}x+\frac{3{p}^{2}}{2}+{{x}_{0}}^{2}$.
联立$\left\{\begin{array}{l}{{x}^{2}=2py}\\{y=\frac{{x}_{0}}{p}x+\frac{3{p}^{2}}{2}+{{x}_{0}}^{2}}\end{array}\right.$,得${x}^{2}+2{x}_{0}x+3{p}^{3}+2p{{x}_{0}}^{2}=0$.
设M(x1,y1),N(x2,y2),MN的中点为(x′,y′),
则$x′=\frac{{x}_{1}+{x}_{2}}{2}=-{x}_{0}$,$y′=-\frac{{{x}_{0}}^{2}}{p}+\frac{3}{2}{p}^{2}+{{x}_{0}}^{2}$,
消去x0,得$y′=\frac{p-1}{p}(x′)^{2}+\frac{3}{2}{p}^{2}$.
∴线段MN中点的轨迹方程为$y=\frac{p-1}{p}{x}^{2}+\frac{3}{2}{p}^{2}$.
点评 本题考查轨迹方程的求法,考查了直线与抛物线位置关系的应用,考查计算能力,是中档题.


科目:高中数学 来源:2016-2017学年河北省高二理上第一次月考数学试卷(解析版) 题型:填空题
某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据,则其线性回归直线方程是______________
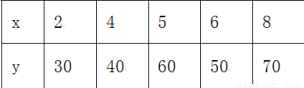
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=\sqrt{x^2}$ | B. | y=lg10x | C. | $y=\frac{x^2}{x}$ | D. | $y={(\sqrt{x-1})^2}+1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com