
分析 由已知求出圆锥的底面半径,进一步求得高,代入圆锥体积公式得答案.
解答 解:半径为1米的半圆的周长为$\frac{1}{2}×2π×1$=π,
则制作成圆锥的底面周长为π,母线长为1,
设圆锥的底面半径为r,则2πr=π,即r=$\frac{1}{2}$.
∴圆锥的高为h=$\sqrt{{1}^{2}-(\frac{1}{2})^{2}}=\frac{\sqrt{3}}{2}$.
∴V=$\frac{1}{3}$×$π×(\frac{1}{2})^{2}×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}π}{24}$(立方米).
故答案为:$\frac{{\sqrt{3}π}}{24}$.
点评 本题考查柱、锥、台体体积的求法,关键是明确圆锥剪展前后的量的关系,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,m、n不平行,则n与α不平行 | B. | 若m∥α,m、n不垂直,则n与α不垂直 | ||
| C. | 若m⊥α,m、n不平行,则n与α不垂直 | D. | 若m⊥α,m、n不垂直,则n与α不平行 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
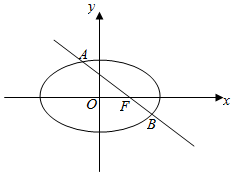 椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$过点M(2,0),且右焦点为F(1,0),过F的直线l与椭圆C相交于A、B两点.设点P(4,3),记PA、PB的斜率分别为k1和k2.
椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$过点M(2,0),且右焦点为F(1,0),过F的直线l与椭圆C相交于A、B两点.设点P(4,3),记PA、PB的斜率分别为k1和k2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{1}{2}})$ | B. | $({\frac{1}{2},1})$ | C. | (0,1) | D. | $({0,\frac{1}{2}})∪$$({\frac{1}{2},1})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com