
【题目】已知椭圆![]() 的短轴长为
的短轴长为![]() ,左右焦点分别为
,左右焦点分别为![]() ,
,![]() ,点
,点![]() 是椭圆上位于第一象限的任一点,且当
是椭圆上位于第一象限的任一点,且当![]() 时,
时,![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若椭圆![]() 上点
上点![]() 与点
与点![]() 关于原点
关于原点![]() 对称,过点
对称,过点![]() 作
作![]() 垂直于
垂直于![]() 轴,垂足为
轴,垂足为![]() ,连接
,连接![]() 并延长交
并延长交![]() 于另一点
于另一点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
(ⅰ)求![]() 面积最大值;
面积最大值;
(ⅱ)证明:直线![]() 与
与![]() 斜率之积为定值.
斜率之积为定值.
科目:高中数学 来源: 题型:
【题目】在以ABCDEF为顶点的五面体中,底面ABCD为菱形,∠ABC=120°,AB=AE=ED=2EF,EF![]() AB,点G为CD中点,平面EAD⊥平面ABCD.
AB,点G为CD中点,平面EAD⊥平面ABCD.
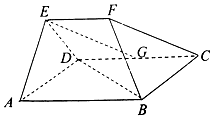
(1)证明:BD⊥EG;
(2)若三棱锥![]() ,求菱形ABCD的边长.
,求菱形ABCD的边长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,上顶点为
,上顶点为![]() ,
,![]() 的面积为1,且椭圆
的面积为1,且椭圆![]() 的离心率为
的离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)点![]() 在椭圆上且位于第二象限,过点
在椭圆上且位于第二象限,过点![]() 作直线
作直线![]() ,过点
,过点![]() 作直线
作直线![]() ,若直线
,若直线![]() 的交点
的交点![]() 恰好也在椭圆
恰好也在椭圆![]() 上,求点
上,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解家长对学校食堂的满意情况,分别从高一、高二年级随机抽取了20位家长的满意度评分,其频数分布表如下:
满意度评分分组 |
|
|
|
|
| 合计 |
高一 | 1 | 3 | 6 | 6 | 4 | 20 |
高二 | 2 | 6 | 5 | 5 | 2 | 20 |
根据评分,将家长的满意度从低到高分为三个等级:
满意度评分 | 评分 | 70 | 评分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
假设两个年级家长的评价结果相互独立,根据所给数据,以事件发生的频率作为相应事件发生的概率.现从高一、高二年级各随机抽取1名家长,记事件![]() :“高一家长的满意度等级高于高二家长的满意度等级”,则事件
:“高一家长的满意度等级高于高二家长的满意度等级”,则事件![]() 发生的概率为__________.
发生的概率为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且![]() ,
, ![]() .
.

求证:(1)直线DE![]() 平面A1C1F;
平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分13分)
某食品厂进行蘑菇的深加工,每公斤蘑菇的成本20元,并且每公斤蘑菇的加工费为![]() 元(
元(![]() 为常数,且
为常数,且![]() ,设该食品厂每公斤蘑菇的出厂价为
,设该食品厂每公斤蘑菇的出厂价为![]() 元(
元(![]() ),根据市场调查,销售量
),根据市场调查,销售量![]() 与
与![]() 成反比,当每公斤蘑菇的出厂价为30元时,日销售量为100公斤.
成反比,当每公斤蘑菇的出厂价为30元时,日销售量为100公斤.
(Ⅰ)求该工厂的每日利润![]() 元与每公斤蘑菇的出厂价
元与每公斤蘑菇的出厂价![]() 元的函数关系式;
元的函数关系式;
(Ⅱ)若![]() ,当每公斤蘑菇的出厂价
,当每公斤蘑菇的出厂价![]() 为多少元时,该工厂的利润
为多少元时,该工厂的利润![]() 最大,并求最大值.
最大,并求最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年10月28日,重庆公交车坠江事件震惊全国,也引发了广大群众的思考——如何做一个文明的乘客.全国各地大部分社区组织居民学习了文明乘车规范.![]() 社区委员会针对居民的学习结果进行了相关的问卷调查,并将得到的分数整理成如图所示的统计图.
社区委员会针对居民的学习结果进行了相关的问卷调查,并将得到的分数整理成如图所示的统计图.
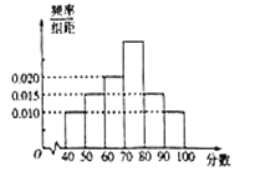
(Ⅰ)求得分在![]() 上的频率;
上的频率;
(Ⅱ)求![]() 社区居民问卷调查的平均得分的估计值;(同一组中的数据以这组数据所在区间中点的值作代表)
社区居民问卷调查的平均得分的估计值;(同一组中的数据以这组数据所在区间中点的值作代表)
(Ⅲ)以频率估计概率,若在全部参与学习的居民中随机抽取5人参加问卷调查,记得分在![]() 间的人数为
间的人数为![]() ,求
,求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2+bln(x+1),其中b≠0.
(1)若b=﹣12,求f(x)在[1,3]的最小值;
(2)如果f(x)在定义域内既有极大值又有极小值,求实数b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com