
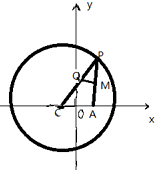
 已知点C为圆(x+1)2+y2=8的圆心,P是圆上的动点,点Q在圆的半径CP上,且有点A(1,0)和AP上的点M,满足$\overrightarrow{MQ}$•$\overrightarrow{AP}$=0,$\overrightarrow{AP}$=2$\overrightarrow{AM}$.
已知点C为圆(x+1)2+y2=8的圆心,P是圆上的动点,点Q在圆的半径CP上,且有点A(1,0)和AP上的点M,满足$\overrightarrow{MQ}$•$\overrightarrow{AP}$=0,$\overrightarrow{AP}$=2$\overrightarrow{AM}$.分析 (1)利用线段的垂直平分线的性质、椭圆的定义即可得出.
(2)设F(x1,y1),H(x2,y2),由直线y=kx+$\sqrt{{k}^{2}+1}$,(k>0)与椭圆联立得$(2{k}^{2}+1){x}^{2}+4k\sqrt{{k}^{2}+1}x+2{k}^{2}$=0,由此利用根的判别式、韦达定理、向量数量积结合已知条件能求出k的取值范围.
解答 解:(1)由题意知MQ中线段AP的垂直平分线,
∴|CP|=|QC|+|QP|=|QC|+|QA|=2$\sqrt{2}$>|CA|=2,
∴点Q的轨迹是以点C,A为焦点,焦距为2,长轴为2$\sqrt{2}$的椭圆,b=1,
故点Q的轨迹方程是$\frac{{x}^{2}}{2}+{y}^{2}$=1.
(II)设F(x1,y1),H(x2,y2),
由直线y=kx+$\sqrt{{k}^{2}+1}$,(k>0)与椭圆联立得$(2{k}^{2}+1){x}^{2}+4k\sqrt{{k}^{2}+1}x+2{k}^{2}$=0,
△=8k2>0,x1+x2=-$\frac{4k\sqrt{{k}^{2}+1}}{2{k}^{2}+1}$,x1x2=$\frac{2{k}^{2}}{2{k}^{2}+1}$,
∴$\overrightarrow{OF}$•$\overrightarrow{OH}$=x1x2+y1y2=$\frac{{k}^{2}+1}{2{k}^{2}+1}$,
∴$\frac{2}{3}$≤$\frac{{k}^{2}+1}{2{k}^{2}+1}$≤$\frac{3}{4}$
即$\frac{1}{2}$≤k2≤1,
∵k>0,∴解得$\frac{\sqrt{2}}{2}≤k≤1$.
点评 本题考查了椭圆的标准方程及其性质、一元二次方程的根与系数的关系、数量积运算性质、不等式的解法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
| 成绩(单位:分) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 数学 | 8 | 12 | 40 | 32 | 8 |
| 物理 | 7 | 18 | 40 | 29 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
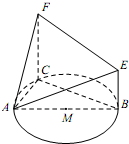 如图,某简单几何体的一个面ABC内接于圆M,AB是圆M的直径,CF∥BE,BE⊥平面ABC,且AB=2,AC=1,BE+CF=7.
如图,某简单几何体的一个面ABC内接于圆M,AB是圆M的直径,CF∥BE,BE⊥平面ABC,且AB=2,AC=1,BE+CF=7.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com