
分析 由题意可知ABCD 是小圆,对角线长为4,四棱锥的高为1,推出球心O到平面ABCD的距离为2,O到PE的距离为$\sqrt{7}$,然后利用勾股定理求出底面ABCD的中心与顶点P之间的距离.
解答 解:由题意可知ABCD 是小圆,对角线长为4,四棱锥的高为1,
点P,A,B,C,D均在半径为2$\sqrt{2}$的同一球面上,
所以球心O到平面ABCD的距离为2,
设PE⊥平面ABCD,O到PE的距离为d,则d=$\sqrt{8-(2-1)^{2}}$=$\sqrt{7}$,
∴底面ABCD的中心与顶点P之间的距离为$\sqrt{7+1}$=2$\sqrt{2}$,
故答案为$2\sqrt{2}$.
点评 本题是中档题,考查球的内接多面体的知识,考查逻辑推理能力,计算能力.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:解答题
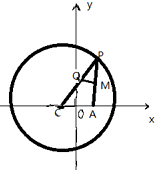 已知点C为圆(x+1)2+y2=8的圆心,P是圆上的动点,点Q在圆的半径CP上,且有点A(1,0)和AP上的点M,满足$\overrightarrow{MQ}$•$\overrightarrow{AP}$=0,$\overrightarrow{AP}$=2$\overrightarrow{AM}$.
已知点C为圆(x+1)2+y2=8的圆心,P是圆上的动点,点Q在圆的半径CP上,且有点A(1,0)和AP上的点M,满足$\overrightarrow{MQ}$•$\overrightarrow{AP}$=0,$\overrightarrow{AP}$=2$\overrightarrow{AM}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5x-12y+38=0 | B. | 5x+12y+38=0 | ||
| C. | 5x-12y+38=0或x=2 | D. | 5x+12y+38=0或x=4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4032π}$ | B. | $\frac{1}{2016π}$ | C. | $\frac{1}{4032}$ | D. | $\frac{1}{2016}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
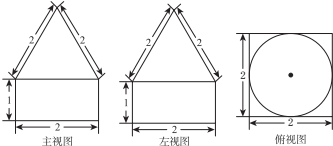
| A. | $2+\frac{{\sqrt{3}}}{3}π$ | B. | $4+\sqrt{3}π$ | C. | $\frac{4}{3}+\frac{{\sqrt{3}}}{3}π$ | D. | $4+\frac{{\sqrt{3}}}{3}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某单位拟建一个扇环形状的花坛(如图所示),按设计要求扇环的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为x米,圆心角为θ(弧度).
某单位拟建一个扇环形状的花坛(如图所示),按设计要求扇环的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为x米,圆心角为θ(弧度).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com