
分析 (1)求出函数的定义域,函数的导数,求出极值点,判断导函数符号,然后求解单调区间.
(2)求出$g'(x)=m+\frac{1}{x}$,x∈(0,e],通过①若m≥0,②若m<0,判断函数的单调性,求解函数的最值,然后求m.
(3)利用x≥1时,$f(x)≥\frac{k}{x+1}$恒成立,分离变量,构造函数$h(x)=lnx+\frac{lnx}{x}+\frac{1}{x}+1$,利用函数的导数,求解函数的最值,推出结果即可.
解答 解:(1)易知f(x)定义域为(0,+∞),$f'(x)=-\frac{lnx}{x^2}$,令f'(x)=0,得x=1.
当0<x<1时,f'(x)>0;当x>1时,f'(x)<0.
∴f(x)在(0,1)上是增函数,在(1,+∞)上是减函数.
(2)∵g(x)=1+lnx+mx,$g'(x)=m+\frac{1}{x}$,x∈(0,e],
①若m≥0,则g'(x)≥0,从而g(x)在(0,e]上是增函数,∴g(x)max=g(e)=me+2≥0,不合题意.
②若m<0,则由g'(x)>0,即$0<x<-\frac{1}{m}$,若$-\frac{1}{m}≥e$,g(x)在(0,e]上是增函数,
由①知不合题意.
由g'(x)<0,即$-\frac{1}{m}<x≤e$.
从而g(x)在$(0,-\frac{1}{m})$上是增函数,在$(-\frac{1}{m},e]$为减函数,
∴$g{(x)_{max}}=g(-\frac{1}{m})=ln(-\frac{1}{m})$,令ln($-\frac{1}{m}$)=-3,所以m=-e3,
∵$-\frac{1}{m}=\frac{1}{e^3}<e$,∴所求的m=-e3.
(3)∵x≥1时,$f(x)≥\frac{k}{x+1}$恒成立,∴k≤(x+1)f(x)=lnx+$\frac{lnx}{x}$+$\frac{1}{x}$+1,
令$h(x)=lnx+\frac{lnx}{x}+\frac{1}{x}+1$,
∴$h'(x)=\frac{x-lnx}{x^2}$恒大于0,
∴h(x)在[1,+∞)为增函数,
∴h(x)min=h(1)=2,∴k≤2.
点评 本题考查函数的导数的综合应用,函数的最值以及函数的单调性的判断,构造法的应用,考查转化思想以及分类讨论思想的应用.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
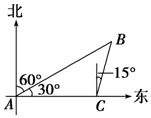 如图,一船以每小时20km的速度向东航行,船在A处看到一个灯塔B在北偏东60°方向,行驶4小时后,船到达C处,看到这个灯塔在北偏东15°方向,这时船与灯塔间的距离为$40\sqrt{2}$km.
如图,一船以每小时20km的速度向东航行,船在A处看到一个灯塔B在北偏东60°方向,行驶4小时后,船到达C处,看到这个灯塔在北偏东15°方向,这时船与灯塔间的距离为$40\sqrt{2}$km.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-\frac{1}{2},\frac{1}{2})$ | B. | $(0,\frac{1}{2})$ | C. | $(\frac{1}{2},1)$ | D. | $(-\frac{1}{2},1)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com