
【题目】一种放射性元素,最初的质量为500克,按每年10%衰减.
(1)求t年后,这种放射性元素的质量w的表达式;
(2)用求出的函数表达式,求这种放射性元素的半衰期.(放射性元素的原子核有半数发生衰变时所需要的时间,叫“半衰期”)(lg0.5≈﹣0.3010,lg0.9≈﹣0.0458,结果精确到0.1).
【答案】
(1)解:最初的质量为500g,
经过1年后,ω=500(1﹣10%)=500×0.91,
经过2年后,ω=500×0.9(1﹣10%)=500×0.92,
由此推知,t年后,ω=500×0.9t,
∴t年后,ω关于t的表达式为ω=500×0.9t
(2)解:根据题意得,解方程500×0.9t=250,0.9t=0.5
∴lg0.9t=lg0.5,∴tlg0.9=lg0.5,
∴t= ![]() ≈6.6(年),
≈6.6(年),
即这种放射性元素的半衰期约为6.6年
【解析】(1)根据最初的质量为500克,按每年10%衰减,可得t年后,这种放射性元素的质量w的表达式;(2)根据题意得,解方程500×0.9t=250,两边取对数,再用换底公式变形,代入已知数据可得x的近似值,四舍五入即可得出正确答案.


科目:高中数学 来源: 题型:
【题目】在“一带一路”的建设中,中石化集团获得了某地深海油田区块的开采权,集团在该地区随机初步勘探了几口井,取得了地质资料.进入全面勘探时期后,集团按网络点来布置井位进行全面勘探.由于勘探一口井的费用很高,如果新设计的井位与原有井位重合或接近,便利用旧井的地质资料,不必打这口新井,以节约勘探费用.勘探初期数据资料下表:

(1)在散点图中![]() 号旧井位置大致分布在一条直线附近,借助前5组数据求得回归线方程为
号旧井位置大致分布在一条直线附近,借助前5组数据求得回归线方程为![]() ,求
,求![]() ,并估计
,并估计![]() 的预报值;
的预报值;
(2)现准备勘探新井![]() ,若通过1、3、5、7号井计算出的
,若通过1、3、5、7号井计算出的![]() 的值(
的值(![]() 精确到0.01)相比于(1)中
精确到0.01)相比于(1)中![]() 的值之差(即:
的值之差(即:![]() )不超过10%,则使用位置最接近的已有旧井
)不超过10%,则使用位置最接近的已有旧井![]() ,否则在新位置打井,请判断可否使用旧井?(参考公式和计算结果:
,否则在新位置打井,请判断可否使用旧井?(参考公式和计算结果: ,
,![]() )
)
(3)设出油量与钻探深度的比值![]() 不低于20的勘探井称为优质井,在原有井号
不低于20的勘探井称为优质井,在原有井号![]() 的井中任意勘探3口井,求恰好2口是优质井的概率.
的井中任意勘探3口井,求恰好2口是优质井的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目.根据预测,甲、乙项目可能的最大盈利率分别为100%和50%,可能的最大亏损分别为30%和10%.投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元.问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x∈R|2x﹣8=0},B={x∈R|x2﹣2(m+1)x+m2=0}
(1)若m=4,求A∪B;
(2)若A∪B=A,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等比数列{an}的前项n和Sn , a2= ![]() ,且S1+
,且S1+ ![]() ,S2 , S3成等差数列,数列{bn}满足bn=2n.
,S2 , S3成等差数列,数列{bn}满足bn=2n.
(1)求数列{an}的通项公式;
(2)设cn=anbn , 若对任意n∈N+ , 不等式c1+c2+…+cn≥ ![]() λ+2Sn﹣1恒成立,求λ的取值范围.
λ+2Sn﹣1恒成立,求λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是首项为a1= ![]() ,公比q=
,公比q= ![]() 的等比数列,设bn+2=3log
的等比数列,设bn+2=3log ![]() an(n∈N*),数列{cn}满足cn=anbn .
an(n∈N*),数列{cn}满足cn=anbn .
(1)求证:{bn}是等差数列;
(2)求数列{cn}的前n项和Sn;
(3)若cn≤ ![]() +m﹣1对一切正整数n恒成立,求实数m的取值范围.
+m﹣1对一切正整数n恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖暅是南北朝时代的伟大科学家,5世纪末提出体积计算原理,即祖暅原理:“幂势既同,则积不容异”.意思是:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任何一个平面所截,如果截面面积都相等,那么这两个几何体的体积一定相等.现有以下四个几何体:图①是从圆柱中挖出一个圆锥所得的几何体;图②、图③、图④分别是圆锥、圆台和半球,则满足祖暅原理的两个几何体为( )
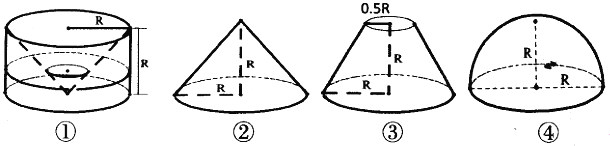
A. ①② B. ①③ C. ②④ D. ①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】山西某公司有一批专业技术人员,对他们进行年龄状况和接受教育程度(本科学历)的调查,其结果(人数分布)如表:
学历 | 35岁以下 | 35 | 50岁以上 |
本科 | 80 | 30 | 20 |
研究生 |
| 20 |
|
(Ⅰ)用分层抽样的方法在![]() 岁年龄段的专业技术人员中抽取一个容量为10的样本,将该样本看成一个总体,从中任取3人,求至少有1人的学历为研究生的概率;
岁年龄段的专业技术人员中抽取一个容量为10的样本,将该样本看成一个总体,从中任取3人,求至少有1人的学历为研究生的概率;
(Ⅱ)在这个公司的专业技术人员中按年龄状况用分层抽样的方法抽取![]() 个人,其中35岁以下48人,50岁以上10人,再从这
个人,其中35岁以下48人,50岁以上10人,再从这![]() 个人中随机抽取出1人,此人的年龄为50岁以上的概率为
个人中随机抽取出1人,此人的年龄为50岁以上的概率为![]() ,求
,求![]() 、
、![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com