

 名学生被考官L面试,求
名学生被考官L面试,求 的分布列和数学期望.
的分布列和数学期望.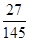 (ⅱ)
(ⅱ)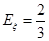
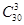 中抽样情况,根据题目要求“学生甲和学生乙恰有一人进入第二轮面试”的事件分为两种情况①甲乙中只有甲入选,即还需要在28人中无序抽样2人,即
中抽样情况,根据题目要求“学生甲和学生乙恰有一人进入第二轮面试”的事件分为两种情况①甲乙中只有甲入选,即还需要在28人中无序抽样2人,即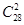 ,②甲乙中只有乙入选,即还需要在28人中无序抽样2人,即
,②甲乙中只有乙入选,即还需要在28人中无序抽样2人,即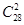 .在利用古典概型概率计算公式即可得到相应的概率
.在利用古典概型概率计算公式即可得到相应的概率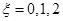 ,再利用组合数算得从6人中无序抽样两人的情况数和分别有0,1,2人是第四组的情况数,即可得到相应的概率,进而得到分布列,在把三种情况的概率与其
,再利用组合数算得从6人中无序抽样两人的情况数和分别有0,1,2人是第四组的情况数,即可得到相应的概率,进而得到分布列,在把三种情况的概率与其 分别相乘再相加即可得到期望.
分别相乘再相加即可得到期望.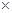 5="0.3;" 第四组的频率为0.04
5="0.3;" 第四组的频率为0.04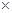 5=0.2;第五组的频率为0.02
5=0.2;第五组的频率为0.02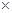 5=0.1. 3分
5=0.1. 3分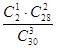 =
=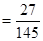 6分
6分 可能的取值为0,1,2. 7分
可能的取值为0,1,2. 7分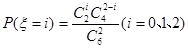 ,则随机变量
,则随机变量 的分布列为:
的分布列为: | 0 | 1 | 2 |
| P | 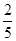 | 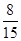 | 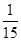 |
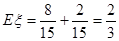


科目:高中数学 来源:不详 题型:解答题
 ,甲、丙两人同时不能被聘用的概率是
,甲、丙两人同时不能被聘用的概率是 ,乙、丙两人同时能被聘用的概率为
,乙、丙两人同时能被聘用的概率为 ,且三人各自能否被聘用相互独立.
,且三人各自能否被聘用相互独立. 为甲、乙、丙三人中能被聘用的人数与不能被聘用的人数之差的绝对值,求
为甲、乙、丙三人中能被聘用的人数与不能被聘用的人数之差的绝对值,求 的分布列与均值(数学期望).
的分布列与均值(数学期望).查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (i=1,2,…,12);设每售出一台电冰箱,电器商获利300元.如销售不出,则每台每月需花保管费100元.问电器商每月初购进多少台电冰箱才能使月平均收益最大?
(i=1,2,…,12);设每售出一台电冰箱,电器商获利300元.如销售不出,则每台每月需花保管费100元.问电器商每月初购进多少台电冰箱才能使月平均收益最大?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,每道程序中得优、良、中的概率分别为p1、
,每道程序中得优、良、中的概率分别为p1、 、p2.
、p2.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的分布列和数学期望.
的分布列和数学期望. 查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 表示小李同学首先摸到黄色乒乓球时的摸球次数,则随机变量
表示小李同学首先摸到黄色乒乓球时的摸球次数,则随机变量 的数学期望值
的数学期望值 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com