
【题目】如图1所示,在梯形![]() 中,
中,![]() //
//![]() ,且
,且![]() ,
,![]() ,分别延长两腰交于点
,分别延长两腰交于点![]() ,点
,点![]() 为线段
为线段![]() 上的一点,将
上的一点,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,如图2所示.
,如图2所示.
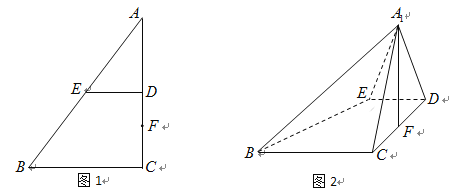
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,四棱锥
,四棱锥![]() 的体积为
的体积为![]() ,求四棱锥
,求四棱锥![]() 的表面积.
的表面积.
【答案】(1)见解析;(2)![]()
【解析】分析:(1)先利用直角三角形和线线平行的性质得到线线垂直,再利用线面垂直的判定定理和性质得到线面垂直和线线垂直;(2)分析四棱锥的各面的形状,利用相关面积公式进行求解.
详解:(1)因为∠C=90°,即AC⊥BC,且DE∥BC,
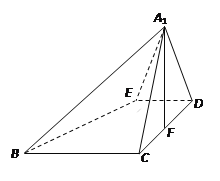
所以DE⊥AC,则DE⊥DC,DE⊥DA1,
又因为DC∩DA1=D,所以DE⊥平面A1DC.
因为A1F平面A1DC,所以DE⊥A1F.
又因为A1F⊥CD,CD∩DE=D,所以A1F⊥平面BCDE,
又因为BE 平面BCDE,所以A1F⊥BE.
(2)由已知DE∥BC,且DE=![]() BC,得D,E分别为AC,AB的中点,
BC,得D,E分别为AC,AB的中点,
在Rt△ABC中,![]() ,则A1E=EB=5,A1D=DC=4,
,则A1E=EB=5,A1D=DC=4,
则梯形BCDE的面积S1=![]() ×(6+3)×4=18,
×(6+3)×4=18,
四棱锥A1—BCDE的体积为V=![]() ×18×A1F=12
×18×A1F=12![]() ,即A1F=2
,即A1F=2![]() ,
,
在Rt△A1DF中,![]() ,即F是CD的中点,
,即F是CD的中点,
所以A1C=A1D=4,
因为DE∥BC,DE⊥平面A1DC,
所以BC⊥平面A1DC,所以BC⊥A1C,所以![]() ,
,
在等腰△A1BE中,底边A1B上的高为![]() ,
,
所以四棱锥A1—BCDE的表面积为S=S1+![]() +
+![]() +
+![]() +
+![]()
=18+![]()
![]() ×4×2
×4×2![]() +
+![]() ×6×4+
×6×4+![]() ×2
×2![]() ×2
×2![]() =36+4
=36+4![]() +2
+2![]() .
.


科目:高中数学 来源: 题型:
【题目】已知等比数列![]() 的首项是1,公比为3,等差数列
的首项是1,公比为3,等差数列![]() 的首项是
的首项是![]() ,公差为1,把
,公差为1,把![]() 中的各项按如下规则依次插入到
中的各项按如下规则依次插入到![]() 的每相邻两项之间,构成新数列
的每相邻两项之间,构成新数列![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…,即在
,…,即在![]() 和
和![]() 两项之间依次插入
两项之间依次插入![]() 中
中![]() 个项,则
个项,则![]() __________.(用数字作答)
__________.(用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】运动健康已成为大家越来越关心的话题,某公司开发的一个类似计步数据库的公众号.手机用户可以通过关注该公众号查看自己每天行走的步数,同时也可以和好友进行运动量的PK和点赞.现从张华的好友中随机选取40人(男、女各20人),记录他们某一天行走的步数,并将数据整理如表:
步数 性别 | 0~2000 | 2001~5000 | 5001~8000 | 8001~10000 | >10000 |
男 | 1 | 2 | 4 | 7 | 6 |
女 | 0 | 3 | 9 | 6 | 2 |
(1)若某人一天行走的步数超过8000步被评定为“积极型”,否则被评定为“懈怠型”,根据题意完成下列2×2列联表,并据此判断能否有90%的把握认为男、女的“评定类型”有差异?
积极型 | 懈怠型 | 总计 | |
男 | |||
女 | |||
总计 |
(2)在张华的这40位好友中,从该天行走的步数不超过5000步的人中随机抽取2人,设抽取的女性有X人,求X=1时的概率.
参考公式与数据:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
K2=![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“新零售”模式的背景下,某大型零售公司咪推广线下分店,计划在![]() 市的
市的![]() 区开设分店,为了确定在该区开设分店的个数,该公司对该市已开设分店听其他区的数据作了初步处理后得到下列表格.记
区开设分店,为了确定在该区开设分店的个数,该公司对该市已开设分店听其他区的数据作了初步处理后得到下列表格.记![]() 表示在各区开设分店的个数,
表示在各区开设分店的个数, ![]() 表示这个
表示这个![]() 个分店的年收入之和.
个分店的年收入之和.
| 2 | 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 | 6 |
(1)该公司已经过初步判断,可用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)假设该公司在![]() 区获得的总年利润
区获得的总年利润![]() (单位:百万元)与
(单位:百万元)与![]() 之间的关系为
之间的关系为![]() ,请结合(1)中的线性回归方程,估算该公司应在
,请结合(1)中的线性回归方程,估算该公司应在![]() 区开设多少个分店时,才能使
区开设多少个分店时,才能使![]() 区平均每个店的年利润最大?
区平均每个店的年利润最大?
(参考公式: ![]() ,其中
,其中 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划购买1台机器,该种机器使用三年后即被淘汰.在购进机器时,可以一次性额外购买几次维修服务,每次维修服务费用200元,另外实际维修一次还需向维修人员支付小费,小费每次50元.在机器使用期间,如果维修次数超过购机时购买的维修服务次数,则每维修一次需支付维修服务费用500元,无需支付小费.现需决策在购买机器时应同时一次性购买几次维修服务,为此搜集并整理了100台这种机器在三年使用期内的维修次数,得下面统计表:
维修次数 | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 20 | 30 | 30 | 10 |
记x表示1台机器在三年使用期内的维修次数,y表示1台机器在维修上所需的费用(单位:元),![]() 表示购机的同时购买的维修服务次数.
表示购机的同时购买的维修服务次数.
(1)若![]() =10,求y与x的函数解析式;
=10,求y与x的函数解析式;
(2)若要求“维修次数不大于![]() ”的频率不小于0.8,求n的最小值;
”的频率不小于0.8,求n的最小值;
(3)假设这100台机器在购机的同时每台都购买10次维修服务,或每台都购买11次维修服务,分别计算这100台机器在维修上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买10次还是11次维修服务?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一条小河岸边有相距![]() 的
的![]() 两个村庄(村庄视为岸边上
两个村庄(村庄视为岸边上![]() 两点),在小河另一侧有一集镇
两点),在小河另一侧有一集镇![]() (集镇视为点
(集镇视为点![]() ),
),![]() 到岸边的距离
到岸边的距离![]() 为
为![]() ,河宽
,河宽![]() 为
为![]() ,通过测量可知,
,通过测量可知,![]() 与
与![]() 的正切值之比为
的正切值之比为![]() .当地政府为方便村民出行,拟在小河上建一座桥
.当地政府为方便村民出行,拟在小河上建一座桥![]() (
(![]() 分别为两岸上的点,且
分别为两岸上的点,且![]() 垂直河岸,
垂直河岸,![]() 在
在![]() 的左侧),建桥要求:两村所有人到集镇所走距离之和最短,已知
的左侧),建桥要求:两村所有人到集镇所走距离之和最短,已知![]() 两村的人口数分别是
两村的人口数分别是![]() 人、
人、![]() 人,假设一年中每人去集镇的次数均为
人,假设一年中每人去集镇的次数均为![]() 次.设
次.设![]() .(小河河岸视为两条平行直线)
.(小河河岸视为两条平行直线)

(1)记![]() 为一年中两村所有人到集镇所走距离之和,试用
为一年中两村所有人到集镇所走距离之和,试用![]() 表示
表示![]() ;
;
(2)试确定![]() 的余弦值,使得
的余弦值,使得![]() 最小,从而符合建桥要求.
最小,从而符合建桥要求.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com