
【题目】已知两定点![]() 和
和![]() ,动点
,动点![]() 在直线
在直线![]() :
:![]() 上移动,椭圆
上移动,椭圆![]() 以
以![]() ,
,![]() 为焦点且经过点
为焦点且经过点![]() ,则椭圆
,则椭圆![]() 的离心率的最大值为__________.
的离心率的最大值为__________.
科目:高中数学 来源: 题型:
【题目】如图1所示,在梯形![]() 中,
中,![]() //
//![]() ,且
,且![]() ,
,![]() ,分别延长两腰交于点
,分别延长两腰交于点![]() ,点
,点![]() 为线段
为线段![]() 上的一点,将
上的一点,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,如图2所示.
,如图2所示.
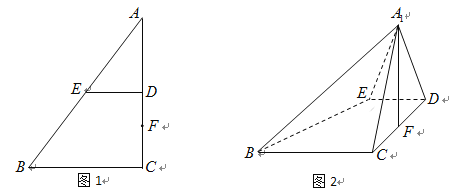
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,四棱锥
,四棱锥![]() 的体积为
的体积为![]() ,求四棱锥
,求四棱锥![]() 的表面积.
的表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴非负半轴为极轴建立极坐标系. 直线
轴非负半轴为极轴建立极坐标系. 直线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(Ⅰ)求圆![]() 的极坐标方程和直线的直角坐标方程;
的极坐标方程和直线的直角坐标方程;
(Ⅱ)射线![]() 与圆
与圆![]() 的交点为
的交点为![]() ,与直线
,与直线![]() 的交点为
的交点为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京101中学校园内有一个“少年湖”,湖的两侧有一个音乐教室和一个图书馆,如图,若设音乐教室在A处,图书馆在B处,为测量A,B两地之间的距离,某同学选定了与A,B不共线的C处,构成△ABC,以下是测量的数据的不同方案:①测量∠A,AC,BC;②测量∠A,∠B,BC;③测量∠C,AC,BC;④测量∠A,∠C,∠B. 其中一定能唯一确定A,B两地之间的距离的所有方案的序号是_______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究机构对高三学生的记忆力![]() 和判断力
和判断力![]() 进行统计分析,得下表数据:
进行统计分析,得下表数据:
| 6 | 8 | 10 | 12 |
| 2 | 3 | 5 | 6 |

(1)请在图中画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)试根据(2)求出的线性回归方程,预测记忆力为9的同学的判断力.
相关公式: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“克拉茨猜想”又称“![]() 猜想”,是德国数学家洛萨克拉茨在1950年世界数学家大会上公布的一个猜想:任给一个正整数
猜想”,是德国数学家洛萨克拉茨在1950年世界数学家大会上公布的一个猜想:任给一个正整数![]() ,如果
,如果![]() 是偶数,就将它减半;如果
是偶数,就将它减半;如果![]() 为奇数就将它乘3加1,不断重复这样的运算,经过有限步后,最终都能够得到1.己知正整数
为奇数就将它乘3加1,不断重复这样的运算,经过有限步后,最终都能够得到1.己知正整数![]() 经过6次运算后得到1,则
经过6次运算后得到1,则![]() 的值为__________.
的值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地西红柿从2月1号起开始上市,通过市场调查,得到西红柿种植成本![]() (单位:元/100
(单位:元/100![]() )与上市时间
)与上市时间![]() (距2月1日的天数,单位:天)的数据如下表:
(距2月1日的天数,单位:天)的数据如下表:
时间 | 50 | 110 | 250 |
成本 | 150 | 108 | 150 |
(1)根据上表数据,从下列函数中选取一个函数描述西红柿种植成本![]() 与上市时间
与上市时间![]() 的变化关系:
的变化关系:![]() ;
;
(2)利用(1)中选取的函数,求西红柿种植成本![]() 最低时的上市天数
最低时的上市天数![]() 及最低种植成本.
及最低种植成本.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com