
| A�� | $��\frac{10}{11}����$ | B�� | $[\frac{10}{11}����$ | C�� | $[��\frac{11}{10}��$ | D�� | $����\frac{11}{10}��$ |
���� �������Ǻ����ı��ǹ�ʽ�������Ͳ���Ͳ����ʽ������֪�ĵ�ʽ�����ݹ���d�ķ�Χ��������ֵ������ǰn���ʽ�����ö��κ����ĶԳ���ķ�Χ�������a1ȡֵ��Χ��
��� �⣺��$\frac{{{{sin}^2}{a_2}-{{cos}^2}{a_2}+{{cos}^2}{a_2}{{cos}^2}{a_7}-{{sin}^2}{a_2}{{sin}^2}{a_7}}}{{sin��{a_4}+{a_5}��}}=1$��
��$\frac{si{n}^{2}{a}_{2}��1-si{n}^{2}{a}_{7}��-co{s}^{2}{a}_{2}��1-co{s}^{2}{a}_{7}��}{sin��{a}_{4}+{a}_{5}��}$=$\frac{si{n}^{2}{a}_{2}co{s}^{2}{a}_{7}-co{s}^{2}{a}_{2}si{n}^{2}{a}_{7}}{sin��{a}_{4}+{a}_{5}��}$
=$\frac{��sin{a}_{2}cos{a}_{7}-cos{a}_{2}sin{a}_{7}����sin{a}_{2}cos{a}_{7}+cos{a}_{2}sin{a}_{7}��}{sin��{a}_{4}+{a}_{5}��}$
=$\frac{sin��{a}_{2}-{a}_{7}��sin��{a}_{2}+{a}_{7}��}{sin��{a}_{4}+{a}_{5}��}$=sin��a2-a7��=sin��-5d��=1
��sin��5d��=-1��
��d�ʣ�-$\frac{1}{2}$��0������5d�ʣ�-$\frac{5}{2}$��0����
��5d=$-\frac{��}{2}$��d=-$\frac{��}{10}$��
��Sn=na1+$\frac{n��n-1��d}{2}$=na1-$\frac{n��n-1��}{2}��\frac{��}{10}$=-$\frac{{n}^{2}}{20}$��+��a1+$\frac{��}{20}$��n��
�Գ��᷽��Ϊn=$\frac{10}{��}$��a1+$\frac{��}{20}$����
������ҽ���n=11ʱ������{an}��ǰn���Snȡ�����ֵ��
��$\frac{21}{2}$��$\frac{10}{��}$��a1+$\frac{��}{20}$����$\frac{23}{2}$����ã��У�a1��$\frac{11��}{10}$��
������a1��ȡֵ��Χ�ǣ��У�$\frac{11��}{10}$����
��ѡ��D��
���� ���⿼���˵Ȳ����е�ͨ�ʽ�����������Ǻ������йع�ʽ�������˵Ȳ����е�ǰn��ͣ�ѵ���˶��κ���ȡ����ֵ�������������˼���������


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | C${\;}_{12}^{10}$��$\frac{3}{8}$��10��$\frac{5}{8}$��2 | B�� | C${\;}_{12}^{9}$��$\frac{3}{8}$��9��$\frac{5}{8}$��2��$\frac{3}{8}$�� | C�� | C${\;}_{11}^{9}$��$\frac{5}{8}$��9��$\frac{3}{8}$��2 | D�� | C${\;}_{11}^{9}$��$\frac{3}{8}$��10��$\frac{5}{8}$��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
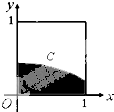 ����ͼ��ʾ�������������ȡһ�㣬��˵�������Ӱ���֣�����C�Ǻ���f��x��=$\frac{1}{\sqrt{2��}}$${\;}^{{e}^{-\frac{{x}^{2}}{2}}}$ ��ͼ�ĸ���Ϊ��������
����ͼ��ʾ�������������ȡһ�㣬��˵�������Ӱ���֣�����C�Ǻ���f��x��=$\frac{1}{\sqrt{2��}}$${\;}^{{e}^{-\frac{{x}^{2}}{2}}}$ ��ͼ�ĸ���Ϊ��������| A�� | 0.2386 | B�� | 0.2718 | C�� | 0.3413 | D�� | 0.4772 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
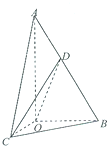 ��ͼ����Rt��AOB�У���OAB=30�㣬б��AB=4��Rt��AOC����ͨ��Rt��AOB��ֱ��AOΪ����ת�õ����Ҷ����B-AO-C��ֱ����ǣ�D��AB���е㣮
��ͼ����Rt��AOB�У���OAB=30�㣬б��AB=4��Rt��AOC����ͨ��Rt��AOB��ֱ��AOΪ����ת�õ����Ҷ����B-AO-C��ֱ����ǣ�D��AB���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com