
【题目】函数![]() 和
和![]() 都是定义在
都是定义在![]() 上的单调减函数,且
上的单调减函数,且![]() ,若对于任意
,若对于任意![]() ,存在
,存在![]() ,
,![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 是
是![]() 在
在![]() 上的“被追逐函数”,若
上的“被追逐函数”,若![]() ,下述四个结论中正确的是( )
,下述四个结论中正确的是( )
①![]() 是
是![]() 在
在![]() 上的“被追逐函数”;
上的“被追逐函数”;
②若![]() 和函数
和函数![]() 关于
关于![]() 轴对称,则
轴对称,则![]() 是
是![]() 在
在![]() 上的“被追逐函数”;
上的“被追逐函数”;
③若![]() 是
是![]() 在
在![]() 上的“被追逐函数”,则
上的“被追逐函数”,则![]() ;
;
④存在![]() ,使得
,使得![]() 是
是![]() 在
在![]() 上的“被追逐函数”.
上的“被追逐函数”.
A.①③④B.①②④C.②③D.①③
【答案】D
【解析】
先判断![]() 与
与![]() 是否单调递减,并求得最小值,再根据若
是否单调递减,并求得最小值,再根据若![]() 是
是![]() 在
在![]() 上的“被追逐函数”,
上的“被追逐函数”,![]() ,则
,则![]() 可用
可用![]() 表示,利用
表示,利用![]() ,代入判断其是否恒成立,即可判断是否满足“被追逐函数”,由此依次判断①②③④
,代入判断其是否恒成立,即可判断是否满足“被追逐函数”,由此依次判断①②③④
对于①,![]() 和
和![]() 在
在![]() 上单调递减,且
上单调递减,且![]() ,
,
若![]() 是
是![]() 在
在![]() 上的“被追逐函数”,则对于任意
上的“被追逐函数”,则对于任意![]() ,存在
,存在![]() ,
,![]() ,使得
,使得![]() 成立,即
成立,即![]() ,所以
,所以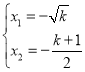 ,
,
此时![]() ,即
,即![]() ,构造函数
,构造函数![]() ,则
,则![]() ,则
,则![]() 在
在![]() 上单调递减,又
上单调递减,又![]() ,则
,则![]() 恒成立,即
恒成立,即![]() ,故对任意
,故对任意![]() ,存在
,存在![]() ,
,![]() ,使得
,使得![]() 成立,故①正确;
成立,故①正确;
对于②,依题意![]() ,则
,则![]() 和
和![]() 在
在![]() 上单调递减,且
上单调递减,且![]() ,若
,若![]() 是
是![]() 在
在![]() 上的“被追逐函数”,则对于任意
上的“被追逐函数”,则对于任意![]() ,存在
,存在![]() ,
,![]() ,使得
,使得![]() 成立,即
成立,即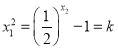 ,所以
,所以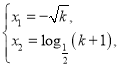 当
当![]() 时,不存在
时,不存在![]() ,
,![]() ,使得
,使得![]() 成立,故②错误;
成立,故②错误;
对于③,若![]() 是
是![]() 在
在![]() 上的“被追逐函数”,此时必有
上的“被追逐函数”,此时必有![]() ,解得
,解得![]() ,当
,当![]() 时,
时,![]() 和
和![]() 在
在![]() 上单调递减,若
上单调递减,若![]() 是
是![]() 在
在![]() 上的“被追逐函数”,则对于任意
上的“被追逐函数”,则对于任意![]() ,存在
,存在![]() ,
,![]() ,使得
,使得![]() 成立,即
成立,即![]() ,所以
,所以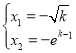 ,即
,即![]() ,则
,则![]() ,构造函数
,构造函数![]() ,则
,则![]() ,则
,则![]() 在
在![]() 上单调递减,又
上单调递减,又![]() ,则
,则![]() 恒成立,即
恒成立,即![]() ,故对任意
,故对任意![]() ,存在
,存在![]() ,
,![]() ,使得
,使得![]() 成立,故③正确;
成立,故③正确;
对于④,当![]() 时,
时,![]() ,而当
,而当![]() 时,
时,![]() ,由
,由![]() 的任意性,不存在
的任意性,不存在![]() ,使得
,使得![]() 是
是![]() 在
在![]() 上的“被追逐函数”,故④错误,
上的“被追逐函数”,故④错误,
故选:D


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源: 题型:
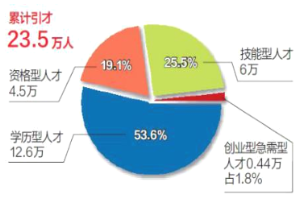
【题目】2020年1月1日《天津日报》发表文章总结天津海河英才计划成果“厚植热土 让天下才天津用”——我市精细服务海河英才优化引才结构.“海河英才”行动计划,紧紧围绕“一基地三区”定位,聚焦战略性新兴产业人才需求,大力、大胆集聚人才.政策实施1年半以来,截至2019年11月30日,累计引进各类人才落户23.5万人.具体比例如图所示,新引进两院院士,长江学者,杰出青年科学基金获得者等顶尖领军人才112人.记者李军计划从人才库中随机选取一部分英才进行跟踪调查采访.
(1)李军抽取了8人其中学历型人才4人,技能型人才3人,资格型人才1人,周二和周五随机进行采访,每天4人(4人顺序任意),周五采访学历型人才人数不超过2人的概率;
(2)李军抽取不同类型的人才有不同的采访补贴,学历型人才500元/人,技能型人才400元/人,资格型人才600元/人,则创业型急需型人才最少补贴多少元/人使每名人才平均采访补贴费用大于等于500元/人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三男生体育课上做投篮球游戏,两人一组,每轮游戏中,每小组两人每人投篮两次,投篮投进的次数之和不少于![]() 次称为“优秀小组”.小明与小亮同一小组,小明、小亮投篮投进的概率分别为
次称为“优秀小组”.小明与小亮同一小组,小明、小亮投篮投进的概率分别为![]() .
.
(1)若![]() ,
,![]() ,则在第一轮游戏他们获“优秀小组”的概率;
,则在第一轮游戏他们获“优秀小组”的概率;
(2)若![]() 则游戏中小明小亮小组要想获得“优秀小组”次数为
则游戏中小明小亮小组要想获得“优秀小组”次数为![]() 次,则理论上至少要进行多少轮游戏才行?并求此时
次,则理论上至少要进行多少轮游戏才行?并求此时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年底,武汉发生“新型冠状病毒”肺炎疫情,国家卫健委紧急部署,从多省调派医务工作者前去支援,正值农历春节举家团圆之际,他们成为“最美逆行者”.武汉市从2月7日起举全市之力入户上门排查确诊的新冠肺炎患者疑似的新冠肺炎患者无法明确排除新冠肺炎的发热患者和确诊患者的密切接触者等“四类”人员,强化网格化管理,不落一户不漏一人.若在排查期间,某小区有5人被确认为“确诊患者的密切接触者”,现医护人员要对这5人随机进行逐一“核糖核酸”检测,只要出现一例阳性,则将该小区确定为“感染高危小区”.假设每人被确诊的概率均为![]() 且相互独立,若当
且相互独立,若当![]() 时,至少检测了4人该小区被确定为“感染高危小区”的概率取得最大值,则
时,至少检测了4人该小区被确定为“感染高危小区”的概率取得最大值,则![]() ____.
____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正四棱锥![]() 的侧棱和底面边长相等,在这个正四棱锥的
的侧棱和底面边长相等,在这个正四棱锥的![]() 条棱中任取两条,按下列方式定义随机变量
条棱中任取两条,按下列方式定义随机变量![]() 的值:
的值:
若这两条棱所在的直线相交,则![]() 的值是这两条棱所在直线的夹角大小(弧度制);
的值是这两条棱所在直线的夹角大小(弧度制);
若这两条棱所在的直线平行,则![]() ;
;
若这两条棱所在的直线异面,则![]() 的值是这两条棱所在直线所成角的大小(弧度制).
的值是这两条棱所在直线所成角的大小(弧度制).
(1)求![]() 的值;
的值;
(2)求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的离心率
的离心率![]() ,左焦点为
,左焦点为![]() ,右顶点为
,右顶点为![]() ,过点
,过点![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,若直线
两点,若直线![]() 垂直于
垂直于![]() 轴时,有
轴时,有![]() .
.
(1)求椭圆的方程;
(2)设直线![]() :
: ![]() 上两点
上两点![]() ,
, ![]() 关于
关于![]() 轴对称,直线
轴对称,直线![]() 与椭圆相交于点
与椭圆相交于点![]() (
(![]() 异于点
异于点![]() ),直线
),直线![]() 与
与![]() 轴相交于点
轴相交于点![]() .若
.若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com