
����Ŀ��2020��1��1�ա�����ձ������������ܽ����Ӣ�żƻ��ɹ�����ֲ���� �����²���������������о�ϸ����Ӣ���Ż����Žṹ.������Ӣ�����ж��ƻ�������Χ����һ������������λ���۽�ս�������˲�ҵ�˲��������������˲�.����ʵʩ1�������������2019��11��30�գ��ۼ����������˲��仧23.5����.���������ͼ��ʾ����������ԺԺʿ������ѧ�ߣ��ܳ������ѧ�������ߵȶ�������˲�112��.��������ƻ����˲ſ������ѡȡһ����Ӣ�Ž��и��ٵ���ɷ�.
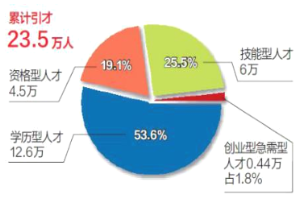
��1�������ȡ��8������ѧ�����˲�4�ˣ��������˲�3�ˣ��ʸ����˲�1�ˣ��ܶ�������������вɷã�ÿ��4�ˣ�4��˳�����⣩������ɷ�ѧ�����˲�����������2�˵ĸ��ʣ�
��2�������ȡ��ͬ���͵��˲��в�ͬ�IJɷò�����ѧ�����˲�500Ԫ/�ˣ��������˲�400Ԫ/�ˣ��ʸ����˲�600Ԫ/�ˣ���ҵ�ͼ������˲����ٲ�������Ԫ/��ʹÿ���˲�ƽ���ɷò������ô��ڵ���500Ԫ/�ˣ�
���𰸡���1��![]() ����2��
����2��![]() Ԫ/��
Ԫ/��
��������
��1������������Լ��ŵ���͵ĸ��ʼ��㹫ʽ�������.
��2���贴ҵ�ͼ������˲����ٲ���![]() Ԫ/�ˣ��г��ֲ��У������ѧ����
Ԫ/�ˣ��г��ֲ��У������ѧ����![]() ��ʹ
��ʹ![]() �ⲻ��ʽ�������.
�ⲻ��ʽ�������.
��1���¼�![]() ������ɷ�ѧ�����˲�����������2�����ĸ���
������ɷ�ѧ�����˲�����������2�����ĸ���![]()
��2�������˲ŵIJ�������Ϊ�������![]() ��
��
ȡֵ�ֱ�Ϊ400��500��600��![]() �ֲ���Ϊ��
�ֲ���Ϊ��
| 400 | 500 | 600 |
|
| 25.5% | 53.6% | 19.1% | 1.8% |
![]()
![]() ����Ϊ
����Ϊ![]() ,
,
���Դ�ҵ�ͼ������˲����ٲ���![]() Ԫ/�ˣ�
Ԫ/�ˣ�
����ʹÿ���˲�ƽ���ɷò������ô��ڵ���500Ԫ/��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
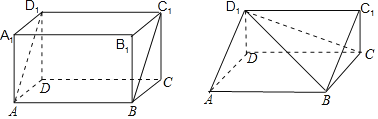
����Ŀ��������ǵ�¡��������MĞ��Щ���ʳ����й��Ŵ���ѧ���������������̹���.�����������MĞ���ҹ��Ŵ���һЩ������ijƺ�.ȡһ��������ͼ������ABCD��A1B1C1D1����ƽ��ABC1D1б��һ��Ϊ�����õ�����һģһ����������.�Ƹ�������Ϊǵ�£�����ǵ�µ�һ��������Ե����ʿ�����������������һ���������Ծ���Ϊ������һ������洹ֱ������D1��ABCD��Ϊ���������µ�����D1��BCC1�����ĸ�ֱ����������ɵ��������Ϊ�MĞ.��֪������ABCD��A1B1C1D1�У�AB��5��BC��4��AA1��3�������ϲ����õ�����.�����������ⳤΪ_____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��GH�Ƕ�������Ĺ�·����ı�Ե�ߣ�ij��˾����GH�ϵ�һ��B�����������A������һ�ֿ⣬��![]() �����ڹ�·���ཨ��߳�Ϊ
�����ڹ�·���ཨ��߳�Ϊ![]() ������������תվCDEF������EF��GH�ϣ����ִӲֿ�A��GH����תվ�ֱ���������·AB,AC,��֪AB=AC+1����
������������תվCDEF������EF��GH�ϣ����ִӲֿ�A��GH����תվ�ֱ���������·AB,AC,��֪AB=AC+1����![]() .
.
��1����![]() ����
����![]() �ĺ�������ʽ�������������
�ĺ�������ʽ�������������
��2�������תվ�Ķ�Χǽ���Ϊ10��Ԫ/km,������·���Ϊ30��Ԫ/km,�ʣ�![]() ȡ��ֵʱ���ù�˾������תվΧǽ��������·�����M���.
ȡ��ֵʱ���ù�˾������תվΧǽ��������·�����M���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() �ֱ�Ϊ��Բ
�ֱ�Ϊ��Բ![]() �����ҽ��㣬
�����ҽ��㣬![]() Ϊ����Բ��һ����ֱ��
Ϊ����Բ��һ����ֱ��![]() ��Ķ��ң�ֱ��
��Ķ��ң�ֱ��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ��ֱ��
��ֱ��![]() ��ֱ��
��ֱ��![]() �Ľ���Ϊ
�Ľ���Ϊ![]() .
.
��1��֤������![]() ������Բ
������Բ![]() ��.
��.
��2����ֱ��![]() ����Բ
����Բ![]() ֻ��һ��������
ֻ��һ��������![]() ��ֱ��
��ֱ��![]() ��ֱ��
��ֱ��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ����ƽ�����Ƿ���ڶ���
����ƽ�����Ƿ���ڶ���![]() ��ʹ��
��ʹ��![]() ������������ڣ�����õ����ꣻ�������ڣ�˵������.
������������ڣ�����õ����ꣻ�������ڣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �ڶ���������������ͬ�ļ�ֵ��.
�ڶ���������������ͬ�ļ�ֵ��.
��1����![]() ��ȡֵ��Χ;
��ȡֵ��Χ;
��2����������ֵ��ֱ�Ϊ��![]() ��
��![]() ��֤��
��֤��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��������,
Ϊ��������,![]() Ϊ
Ϊ![]() �Ḻ�����ϵ�һ������,����
�Ḻ�����ϵ�һ������,����![]() ����
����![]() ,���߶�
,���߶�![]() ���е���
�����![]() ����.
����.
��1����![]() �Ĺ켣
�Ĺ켣![]() �ķ��̣�
�ķ��̣�
��2����![]() ����
Ϊ����![]() ��һ�����ң�
��һ�����ң�![]() ����ֱ��
����ֱ��![]() �ᣩ.�䴹ֱƽ������
�ᣩ.�䴹ֱƽ������![]() �ύ�ڵ�
�ύ�ڵ�![]() .��
.��![]() ʱ,��
ʱ,��![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABC��A1B1C1�У�����BB1C1CΪ���Σ�![]() ��
��
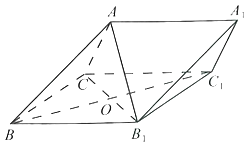
��1����֤��B1C��AB��
��2������CBB1��60�㣬AC��BC���ҵ�A�ڲ���BB1C1C�ϵ�ͶӰΪ��O��������B��AA1��C������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������![]() �У�P��Q��M��N��H��R�Ǹ�������е�.
�У�P��Q��M��N��H��R�Ǹ�������е�.
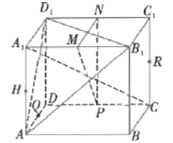
��ֱ��![]() ƽ��
ƽ��![]() ����
����![]() ����P��Q��H��R�ĵ㹲�棻��
����P��Q��H��R�ĵ㹲�棻��![]() ƽ��
ƽ��![]() .������ȷ�ĸ���Ϊ�� ��
.������ȷ�ĸ���Ϊ�� ��
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() ��
��![]() ���Ƕ�����
���Ƕ�����![]() �ϵĵ�������������
�ϵĵ�������������![]() ������������
������������![]() ������
������![]() ��
��![]() ��ʹ��
��ʹ��![]() ���������
���������![]() ��
��![]() ��
��![]() �ϵ���������������
�ϵ���������������![]() �������ĸ���������ȷ���ǣ� ��
�������ĸ���������ȷ���ǣ� ��
��![]() ��
��![]() ��
��![]() �ϵ�������������
�ϵ�������������
����![]() �ͺ���
�ͺ���![]() ����
����![]() ��Գƣ���
��Գƣ���![]() ��
��![]() ��
��![]() �ϵ�������������
�ϵ�������������
����![]() ��
��![]() ��
��![]() �ϵ���������������
�ϵ���������������![]() ��
��
�ܴ���![]() ��ʹ��
��ʹ��![]() ��
��![]() ��
��![]() �ϵ�����������.
�ϵ�����������.
A.�٢ۢ�B.�٢ڢ�C.�ڢ�D.�٢�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com