
【题目】已知定点![]() (
(![]() 为正常数),
为正常数),![]() 为
为![]() 轴负半轴上的一个动点,动点
轴负半轴上的一个动点,动点![]() 满足
满足![]() ,且线段
,且线段![]() 的中点在
的中点在![]() 轴上.
轴上.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设![]() 为曲线
为曲线![]() 的一条动弦(
的一条动弦(![]() 不垂直于
不垂直于![]() 轴).其垂直平分线与
轴).其垂直平分线与![]() 轴交于点
轴交于点![]() .当
.当![]() 时,求
时,求![]() 的最大值.
的最大值.
【答案】(1)![]() (2)6
(2)6
【解析】
(1)设![]() ,进而求得
,进而求得![]() 的坐标,再根据三角形的性质可得
的坐标,再根据三角形的性质可得![]() 即可得
即可得![]() 满足的方程,化简即可.
满足的方程,化简即可.
(2)由(1)以及![]() 可得轨迹
可得轨迹![]() 的方程为
的方程为![]() ,再设弦
,再设弦![]() 所在直线方程为
所在直线方程为![]() ,
,![]() ,
,![]() ,联立直线与抛物线的方程,利用韦达定理求得
,联立直线与抛物线的方程,利用韦达定理求得![]() 的中点,进而求得线段
的中点,进而求得线段![]() 的垂直平分线的方程,代入
的垂直平分线的方程,代入![]() 得到
得到![]() ,再根据弦长公式求解
,再根据弦长公式求解![]() ,代入
,代入![]() 利用二次不等式的最值求解即可.
利用二次不等式的最值求解即可.
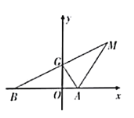
解:(1)设![]() ,则
,则![]() 的中点
的中点![]() 的坐标为
的坐标为![]() ,
,![]() .
.
又![]() ,故
,故![]() .
.
由题意知![]() ,所以
,所以![]() ,即
,即![]() ,所以
,所以![]() .
.
因为![]() 点不能在
点不能在![]() 轴上,故曲线
轴上,故曲线![]() 的方程为
的方程为![]() .
.
(2)设弦![]() 所在直线方程为
所在直线方程为![]() ,
,![]() ,
,![]() .
.
由![]() 得
得![]() .①
.①
则![]() ,
,![]() ,则线段
,则线段![]() 的中点为
的中点为![]() ,
,
即![]() .
.
线段![]() 的垂直平分线的方程为
的垂直平分线的方程为![]() .
.
令![]() ,
,![]() ,得
,得![]() .得
.得![]() .
.
所以![]()
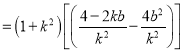
![]()
由①,![]()
![]() .
.
得![]() ,即
,即![]() .
.
所以,当![]() ,即
,即![]() 时,
时,![]() 取得最大值,最大值等于36,即
取得最大值,最大值等于36,即![]() 的最大值为6.
的最大值为6.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知点A(0,2),B为抛物线x2=2y﹣2上任意一点,且B为AC的中点,设动点C的轨迹为曲线E.
(1)求曲线E的方程;
(2)是否存在斜率为1的直线l交曲线E于M、N两点,使得△MAN为以MN为底边的等腰三角形?若存在,请求出l的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年1月1日《天津日报》发表文章总结天津海河英才计划成果“厚植热土 让天下才天津用”——我市精细服务海河英才优化引才结构.“海河英才”行动计划,紧紧围绕“一基地三区”定位,聚焦战略性新兴产业人才需求,大力、大胆集聚人才.政策实施1年半以来,截至2019年11月30日,累计引进各类人才落户23.5万人.具体比例如图所示,新引进两院院士,长江学者,杰出青年科学基金获得者等顶尖领军人才112人.记者李军计划从人才库中随机选取一部分英才进行跟踪调查采访.
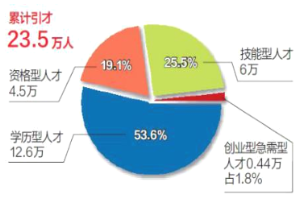
(1)李军抽取了8人其中学历型人才4人,技能型人才3人,资格型人才1人,周二和周五随机进行采访,每天4人(4人顺序任意),周五采访学历型人才人数不超过2人的概率;
(2)李军抽取不同类型的人才有不同的采访补贴,学历型人才500元/人,技能型人才400元/人,资格型人才600元/人,则创业型急需型人才最少补贴多少元/人使每名人才平均采访补贴费用大于等于500元/人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若关于x的不等式e2x﹣alnx![]() a恒成立,则实数a的取值范围是( )
a恒成立,则实数a的取值范围是( )
A.[0,2e]B.(﹣∞,2e]C.[0,2e2]D.(﹣∞,2e2]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+1|﹣|2x﹣2|的最大值为M,正实数a,b满足a+b=M.
(1)求2a2+b2的最小值;
(2)求证:aabb≥ab.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,曲线![]() :
:![]() (α为参数)经过伸缩变换
(α为参数)经过伸缩变换![]() 得到曲线
得到曲线![]() ,在以坐标原点为极点,x轴的正半轴为极轴的极坐标系中,直线l的极坐标方程为
,在以坐标原点为极点,x轴的正半轴为极轴的极坐标系中,直线l的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程;
的普通方程;
(2)设点P是曲线![]() 上的动点,求点P到直线l距离d的最大值.
上的动点,求点P到直线l距离d的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com