
分析 (1)设n所对角为A,n+2所对角为C,运用三角形的余弦定理,化简可得cosA;由正弦定理和二倍角的正弦公式,化简整理可得cosA;
(2)由(1)可得n的方程,可得$\frac{n+2}{2n}=\frac{n+5}{2(n+2)}$,解方程可得n的值.
解答 解:(1)根据大角对大边及大边对大角可知,设n所对角为A,n+2所对角为C,
由余弦定理得:$cosA=\frac{{{{(n+1)}^2}+{{(n+2)}^2}-{n^2}}}{2(n+1)(n+2)}=\frac{n+5}{2(n+2)}$,
由正弦定理得:$\frac{n}{sinA}=\frac{n+2}{sinC}$及C=2A得
$\frac{n}{sinA}$=$\frac{n+2}{sin2A}$=$\frac{n+2}{2sinAcosA}$,
可得$cosA=\frac{n+2}{2n}$;
(2)由(1)可得$\frac{n+2}{2n}=\frac{n+5}{2(n+2)}$得
(n+2)2=n(n+5),
解得n=4.
点评 本题考查解三角形的正弦定理和余弦定理的运用,同时考查二倍角的正弦公式和运算求解能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
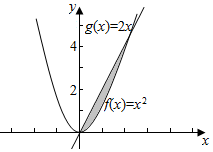
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{3}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
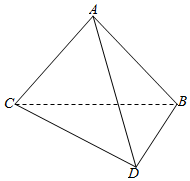 如图,将一副三角板拼接,使他们有公共边BC,且使这两个三角形所在的平面互相垂直,∠BAC=∠CBD=90°,AB=AC,∠BCD=30°,BC=6.
如图,将一副三角板拼接,使他们有公共边BC,且使这两个三角形所在的平面互相垂直,∠BAC=∠CBD=90°,AB=AC,∠BCD=30°,BC=6.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com