
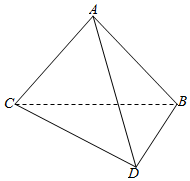
 如图,将一副三角板拼接,使他们有公共边BC,且使这两个三角形所在的平面互相垂直,∠BAC=∠CBD=90°,AB=AC,∠BCD=30°,BC=6.
如图,将一副三角板拼接,使他们有公共边BC,且使这两个三角形所在的平面互相垂直,∠BAC=∠CBD=90°,AB=AC,∠BCD=30°,BC=6.分析 (Ⅰ)利用平面BCD⊥平面ABC,证明BD⊥平面ABC,可证DB⊥AB;
(Ⅱ)利用等体积,能求出C到平面ADB的距离.
解答 (Ⅰ)证明:∵平面BCD⊥平面ABC,BD⊥BC,平面BCD∩平面ABC=BC
∴BD⊥平面ABC,
∵AB?平面ABC,
∴DB⊥AB;
(Ⅱ)解:由(I)BD⊥平面ABC,
∵S△ABC=$\frac{1}{4}×36$=9,DB=$\frac{6}{\sqrt{3}}$=2$\sqrt{3}$,
∴VD-ABC=$\frac{1}{3}×9×2\sqrt{3}$=6$\sqrt{3}$,
∵△ADB是直角三角形,AB=$\frac{6}{\sqrt{2}}$=3$\sqrt{2}$,DB=2$\sqrt{3}$,
∴S△ADB=$\frac{1}{2}×3\sqrt{2}×2\sqrt{3}$=3$\sqrt{6}$.
设点C到平面ADB的距离为h,则$\frac{1}{3}•3\sqrt{6}•h=6\sqrt{3}$,
∴h=3$\sqrt{2}$,
∴点C到平面ADB的距离为3$\sqrt{2}$.
点评 本题考查平面与平面垂直的证明,考查点到平面的距离的求法,是中档题,正确运用等体积法是关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 已知cos θ•tan θ<0,那么角θ是第三或第四象限角 | |
| B. | 函数y=2cos(2x+$\frac{π}{3}$)的图象关于x=$\frac{π}{12}$对称 | |
| C. | sin20°cos10°-cos160°sin10°=$\frac{1}{2}$ | |
| D. | 函数y=|sinx|是周期函数,且周期为π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,+∞) | B. | (-1,3) | C. | [3,+∞) | D. | (-1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {3} | B. | {0,1} | C. | {1,2,3} | D. | {0,1,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,$\frac{5}{2}$] | B. | [-1,4] | C. | [-5,5] | D. | [-3,7] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com