
���� ������λ������������ֵ����������ʽ�����⣮
��� �⣺�ټأ�5�����ݵ���λ��Ϊ24������Ϊ22��
����ǰ������Ϊ22��22��23������������϶�����23���ʼشӴ��������ļ����ʢٳ�����
���ҵأ�5�����ݵ���λ��Ϊ27�������ֵΪ24��
�����ҵ��ܶ෴�����磺18��19��27��28��28�����ҵ�û�дӴ��������ļ����ʢڲ�������
��5����������һ��������32�������ֵΪ26�����巽��Ϊ10.8����x1��x2��x3��x4��
$\frac{1}{5}$[��x1-26��2+��x2-26��2+��x3-26��2+��x4-26��2+62]=10.2��
�ࣨx1-26��2+��x2-26��2+��x3-26��2+��x4-26��2=15��
�ࣨx1-26��2��15��
��|x1-26|��$\sqrt{15}$����x1��26-$\sqrt{15}$��22������شӴ��������ļ����ʢ۳�����
�ඨ�����ļ��ĵ����мͱ�2��������
�ʴ�Ϊ��2��
���� ������Ҫ�����������������������λ����������ƽ���������������ô������������ݵ������������е��⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
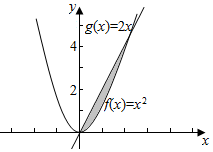
| A�� | $\frac{1}{2}$ | B�� | $\frac{2}{3}$ | C�� | $\frac{4}{3}$ | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
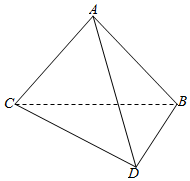 ��ͼ����һ�����ǰ�ƴ�ӣ�ʹ�����й�����BC����ʹ���������������ڵ�ƽ�滥�ഹֱ����BAC=��CBD=90�㣬AB=AC����BCD=30�㣬BC=6��
��ͼ����һ�����ǰ�ƴ�ӣ�ʹ�����й�����BC����ʹ���������������ڵ�ƽ�滥�ഹֱ����BAC=��CBD=90�㣬AB=AC����BCD=30�㣬BC=6���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 10 | B�� | 7 | C�� | 10��4 | D�� | 7��5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | $\sqrt{3}$ | C�� | $\sqrt{2}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {x|x��-1��x��1} | B�� | {x|x��0��x��2} | C�� | {x|x��0��x��1} | D�� | {x|x��0��x��2} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com