Question

20．如图，三棱锥C-ABD中，AB=AD=BD=BC=CD=2，O为BD的中点，∠AOC=120°，P为AC上一点，Q为AO上一点，且$\frac{AP}{PC}$=$\frac{AQ}{QO}$=2．
（Ⅰ）求证：PQ∥平面BCD；
（Ⅱ）求证：PO⊥平面ABD；
（Ⅲ）求四面体ABCD的体积．

Answer 1

分析 （Ⅰ）证明：PQ∥CO，利用线面平行的判定定理证明PQ∥平面BCD；
（Ⅱ）证明BD⊥PO，OP⊥OA，即可证明：PO⊥平面ABD；
（Ⅲ）求出P-ABD的体积，即可求四面体ABCD的体积．

解答 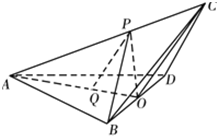（Ⅰ）证明：∵$\frac{AP}{PC}=\frac{AQ}{QO}$，∴PQ∥CO
又∵PQ?平面BCD，CO?平面BCD，
∴PQ∥平面BCD…（4分）
（Ⅱ）证明：由等边△ABD，等边△BCD，O为BD的中点得：BD⊥AO，BD⊥OC，AO∩OC=O，
∴BD⊥平面AOC．
又∵PO?平面AOC，∴BD⊥PO
在△AOC中，∠AOC=120°，$AO=OC=\sqrt{3}$，
∴∠OAC=30°，$AC=\sqrt{O{A^2}+O{C^2}-2•OA•OC•cos{{120}°}}=3$…（7分）
∴AP=2
在△AOP中，由余弦定理得：OP=1…（8分）
∴OP⊥OA…（9分）
又OA∩BD=O，
∴PO⊥平面ABD…（10分）
（Ⅲ）解：∵PO⊥平面ABD，
$\begin{array}{l}{V_{P-ABD}}=\frac{1}{3}{S_{△ABD}}•PO=\frac{1}{3}•\frac{{\sqrt{3}}}{4}A{B^2}•PO\\=\frac{1}{3}•\frac{{\sqrt{3}}}{4}•4•1=\frac{{\sqrt{3}}}{3}\end{array}$
∵$\frac{CA}{CP}=\frac{3}{2}$
∴${V_{C-ABD}}=\frac{3}{2}{V_{P-ABD}}=\frac{3}{2}×\frac{{\sqrt{3}}}{3}=\frac{{\sqrt{3}}}{2}$…（14分）

点评 本题考查线面平行、线面垂直的证明，考查体积的计算，正确运用线面平行、线面垂直的判定定理是关键．