(本小题满分12分)
解:法1:(Ⅰ)过A点作AP,使AP∥DD
1,且AP=DD
1,
连接A
1P,B
1P,如图所示
则∠B
1AP为异面直线AB
1与DD
1所成的角.
∴
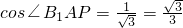
.…(3分)
(Ⅱ)∵F为AD的中点,∴BC⊥平面FB
1A
1,
从而BC⊥FB
1.…(5分)
∵FB
12+GB
12=2a
2+2a
2=4a
2=FG
2,…(6分)
FB
1⊥GB
1∴FB
1⊥平面BCC
1B
1.…(7分)
(Ⅲ)由B
1C
1⊥平面CDD
1C
1,得B
1C
1⊥CC
1.
又由(2)FB
1⊥平面BCC
1B
1,∴由三垂线定理得,FC
1⊥CC
1,
∴∠FC
1B
1是二面角F-CC
1-B的平面角.…(10分)
∵
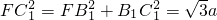
,∴
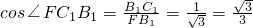
.
即二面角F-CC
1-B的余弦值为

.…(12分)
法2:以D为坐标原点,DA,DC,DD
1所在直线分别为x,y,z轴建立直角坐标系.…(2分)
(Ⅰ)∵
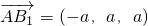
,
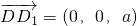
,
∴
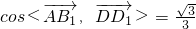
.…(3分)
(Ⅱ)∵
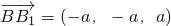
,
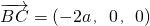
,
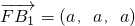
.…(6分)
∴
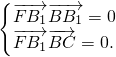
∴FB
1⊥平面BCC
1B
1.…(7分)
(Ⅲ)由(2)知,
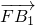
为平面BCC
1B
1的一个法向量.
设
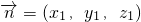
为平面FCC
1的一个法向量,则
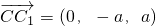
,
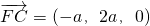
.
由
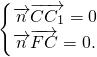
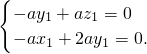
令y
1=1,?x
1=2,z
1=1.
∴
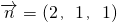
.…(10分)
∴
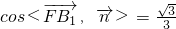
,即二面角F-CC
1-B的余弦值为

.…(12分)
分析:解法1(几何法):(I)过A点作AP,使AP∥DD
1,且AP=DD
1,连接A
1P,B
1P,可得∠B
1AP为异面直线AB
1与DD
1所成的角,解三角形B
1AP,即可得到异面直线AB
1与DD
1所成的角的余弦值;
(Ⅱ)由F为AD的中点,结合上、下两个底面ABCD和A
1B
1C
1D
1互相平行,且都是正方形,DD
1⊥底面ABCD,AB=2A
1B
1=2DD
1=2a,我们易得BC⊥FB
1,FB
1⊥GB
1,由线面垂直的判定定理可得FB
1⊥平面BCC
1B
1;
(Ⅲ)由(II)的结论,我们可得∠FC
1B
1是二面角F-CC
1-B的平面角,解三角形FC
1B
1即可得到二面角F-CC
1-B的余弦值.
解法2(向量法):(I)以D为坐标原点,DA,DC,DD
1所在直线分别为x,y,z轴建立直角坐标系,分别求出异面直线AB
1与DD
1的方向向量,代入向量夹角公式,即可得到异面直线AB
1与DD
1所成的角的余弦值;
(Ⅱ)分别求出向量
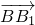
,

,
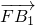
的坐标,根据
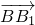
•
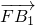
=0,

•
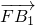
=0,我们可得
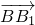
⊥
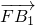
,且

⊥
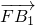
,再由线面垂直的判定定理得到FB
1⊥平面BCC
1B
1;
(Ⅲ)由(II)可得
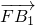
即为平面BCC
1B
1的一个法向量,求出平面FCC
1的一个法向量,代入向量夹角公式,即可得到二面角F-CC
1-B的余弦值.
点评:本题考查的知识点是与二面角有关的立体几何综合题,异面直线及其所成的角,直线与平面垂直的判定,其中解法1 (几何法)的关键是求出线面夹角及二面角的平面角,解法2(向量法)的关键是建立空间坐标系,将空间线面夹角,二面角及线面垂直问题转化为向量夹角问题.

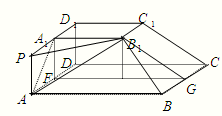
 如图,在多面体ABCD-A1B1C1D1中,上、下两个底面ABCD和A1B1C1D1互相平行,且都是正方形,DD1⊥底面ABCD,AB=2A1B1=2DD1=2a.
如图,在多面体ABCD-A1B1C1D1中,上、下两个底面ABCD和A1B1C1D1互相平行,且都是正方形,DD1⊥底面ABCD,AB=2A1B1=2DD1=2a.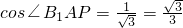 .…(3分)
.…(3分)
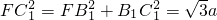 ,∴
,∴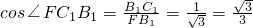 .
. .…(12分)
.…(12分)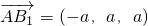 ,
,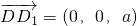 ,
,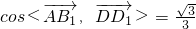 .…(3分)
.…(3分)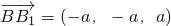 ,
,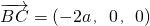 ,
,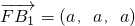 .…(6分)
.…(6分)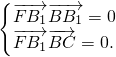
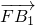 为平面BCC1B1的一个法向量.
为平面BCC1B1的一个法向量.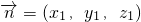 为平面FCC1的一个法向量,则
为平面FCC1的一个法向量,则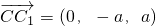 ,
,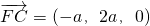 .
.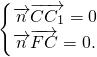
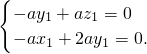 令y1=1,?x1=2,z1=1.
令y1=1,?x1=2,z1=1.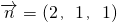 .…(10分)
.…(10分)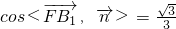 ,即二面角F-CC1-B的余弦值为
,即二面角F-CC1-B的余弦值为 .…(12分)
.…(12分) ,
, ,
, 的坐标,根据
的坐标,根据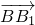 •
•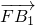 =0,
=0, •
•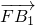 =0,我们可得
=0,我们可得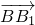 ⊥
⊥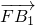 ,且
,且 ⊥
⊥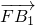 ,再由线面垂直的判定定理得到FB1⊥平面BCC1B1;
,再由线面垂直的判定定理得到FB1⊥平面BCC1B1;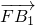 即为平面BCC1B1的一个法向量,求出平面FCC1的一个法向量,代入向量夹角公式,即可得到二面角F-CC1-B的余弦值.
即为平面BCC1B1的一个法向量,求出平面FCC1的一个法向量,代入向量夹角公式,即可得到二面角F-CC1-B的余弦值.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案 如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1
如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1 如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=
如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC= (2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,B1C1=
(2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,B1C1= (2012•合肥一模)如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1⊥平面ABC,AA1∥=BB1,AB=AC=AA1=
(2012•合肥一模)如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1⊥平面ABC,AA1∥=BB1,AB=AC=AA1= (2012•郑州二模)如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=
(2012•郑州二模)如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=