
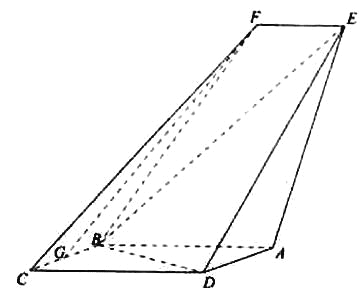
【题目】如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF||AB,AB=2,BC=EF=1,AE=![]() ,DE=3,∠BAD=60,G为BC的中点.
,DE=3,∠BAD=60,G为BC的中点.
(Ⅰ)求证:FG||平面BED;
(Ⅱ)求证:平面BED⊥平面AED;
(Ⅲ)求直线EF与平面BED所成角的正弦值.
【答案】(Ⅰ)详见解析(Ⅱ)详见解析(Ⅲ)![]()
【解析】
试题(Ⅰ)证明线面平行,一般利用线面平行判定定理,即从线线平行出发给予证明,而线线平行寻找与论证,往往结合平几知识,如本题构造一个平行四边形:取![]() 的中点为
的中点为![]() ,可证四边形
,可证四边形![]() 是平行四边形,从而得出
是平行四边形,从而得出![]() (Ⅱ)面面垂直的证明,一般转化为证线面垂直,而线面垂直的证明,往往需多次利用线面垂直判定与性质定理,而线线垂直的证明有时需要利用平几条件,如本题可由余弦定理解出
(Ⅱ)面面垂直的证明,一般转化为证线面垂直,而线面垂直的证明,往往需多次利用线面垂直判定与性质定理,而线线垂直的证明有时需要利用平几条件,如本题可由余弦定理解出![]() ,即
,即![]() (Ⅲ)求线面角,关键作出射影,即面的垂线,可利用面面垂直的性质定理得到线面垂直,即面的垂线:过点
(Ⅲ)求线面角,关键作出射影,即面的垂线,可利用面面垂直的性质定理得到线面垂直,即面的垂线:过点![]() 作
作![]() 于点
于点![]() ,则
,则![]() 平面
平面![]() ,从而直线
,从而直线![]() 与平面
与平面![]() 所成角即为
所成角即为![]() .再结合三角形可求得正弦值
.再结合三角形可求得正弦值
试题解析:(Ⅰ)证明:取![]() 的中点为
的中点为![]() ,连接
,连接![]() ,在
,在![]() 中,因为
中,因为![]() 是
是![]() 的中点,所以
的中点,所以![]() 且
且![]() ,又因为
,又因为![]() ,所以
,所以![]() 且
且![]()
,即四边形![]() 是平行四边形,所以
是平行四边形,所以![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(Ⅱ)证明:在![]() 中,
中,![]() ,由余弦定理可
,由余弦定理可![]() ,进而可得
,进而可得![]() ,即
,即![]() ,又因为平面
,又因为平面![]() 平面
平面![]() 平面
平面![]() ;平面
;平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .又因为
.又因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(Ⅲ)解:因为![]() ,所以直线
,所以直线![]() 与平面
与平面![]() 所成角即为直线
所成角即为直线![]() 与平面
与平面![]() 所成角.过点
所成角.过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,又因为平面
,又因为平面![]() 平面
平面![]() ,由(Ⅱ)知
,由(Ⅱ)知![]() 平面
平面![]() ,所以直线
,所以直线![]() 与平面
与平面![]() 所成角即为
所成角即为![]() .在
.在![]() 中,
中,![]() ,由余弦定理可得
,由余弦定理可得![]() ,所以
,所以![]() ,因此
,因此![]() ,在
,在![]() 中,
中,![]() ,所以直线
,所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]()


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:高中数学 来源: 题型:
【题目】土笋冻是闽南种广受欢迎的特色传统风味小吃某小区超市销售一款土笋冻,进价为每个15元,售价为每个20元.销售的方案是当天进货,当天销售,未售出的全部由厂家以每个10元的价格回购处理.根据该小区以往的销售情况,得到如图所示的频率分布直方图:

(1)估算该小区土笋冻日需求量的平均数![]() (同一组中的数据用该组区间的中点值代表);
(同一组中的数据用该组区间的中点值代表);
(2)已知该超市某天购进了150个土笋冻,假设当天的需求量为![]() 个
个![]() 销售利润为
销售利润为![]() 元.
元.
(i)求关于![]() 的函数关系式;
的函数关系式;
(ii)结合上述频率分布直方图,以额率估计概率的思想,估计当天利润![]() 不小于650元的概率.
不小于650元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
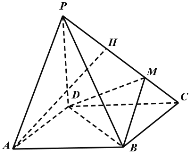
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,点
是菱形,点![]() 在线段PC上,且三棱锥
在线段PC上,且三棱锥![]() 的体积是四棱锥
的体积是四棱锥![]() 的体积的
的体积的![]() ,
,![]() ,
,![]() 平面
平面![]() .
.
(1)若![]() 是
是![]() 的中点,证明:直线
的中点,证明:直线![]() ∥平面
∥平面![]() ;
;
(2)求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为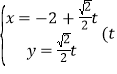 为参数
为参数![]() ,直线
,直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 两点.
两点.
(1)若点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值;
的值;
(2)求曲线![]() 的内接矩形周长的最大值.
的内接矩形周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC-A1B1C1中,点M,N分别为线段A1B,B1C的中点.

(1)求证:MN∥平面AA1C1C;
(2)若∠ABC=90°,AB=BC=2,AA1=3,求点B1到面A1BC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地随着经济的发展,居民收入逐年增长该地一建设银行统计连续五年的储蓄存款(年底余额)得到下表:
年份x | 2014 | 2015 | 2016 | 2017 | 2018 |
储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
为便于计算,工作人员将上表的数据进行了处理(令![]()
![]() ),得到下表:
),得到下表:
时间t | 1 | 2 | 3 | 4 | 5 |
储蓄存款z | 0 | 1 | 2 | 3 | 5 |
(1)求z关于t的线性回归方程;
(2)通过(1)中的方程,求出y关于x的回归方程;
(3)用所求回归方程预测到2020年年底,该地储蓄存款额可达多少?
附:线性回归方程![]() ,其中
,其中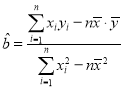 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 及圆
及圆![]() .
.
(1)若直线![]() 过点
过点![]() 且与圆心
且与圆心![]() 的距离为1,求直线
的距离为1,求直线![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于
交于![]() 两点,当
两点,当![]() 时,求以线段
时,求以线段![]() 为直径的圆
为直径的圆![]() 的方程;
的方程;
(3)设直线![]() 与圆
与圆![]() 交于
交于![]() 两点,是否存在实数
两点,是否存在实数![]() ,使得过点
,使得过点![]() 的直线
的直线![]() 垂直平分弦
垂直平分弦![]() ?若存在,求出实数
?若存在,求出实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com