
分析 把已知方程组中第一式变形,得到2y+z=x+2u≥2$\sqrt{2xu}$,结合第二式得到2y+z≥4$\sqrt{yz}$,两边同时除以y,得到关于$\sqrt{\frac{z}{y}}$的不等式,换元后求解不等式得到$\sqrt{\frac{z}{y}}$的范围,则答案可求.
解答 解:由题意,2y+z=x+2u≥2$\sqrt{2xu}$=4$\sqrt{yz}$,
∴2+$\frac{z}{y}$≥4$\sqrt{\frac{z}{y}}$,
令t=$\sqrt{\frac{z}{y}}$,则t≥1,2+t2≥4t,
∴t2-4t+2≥0,
∵t≥1,
∴t≥2+$\sqrt{2}$,
∴$\frac{z}{y}$=t2≥6+4$\sqrt{2}$,
∵存在正实数M,且满足M≤$\frac{z}{y}$,
∴M≤6+4$\sqrt{2}$,
∴M的最大值是6+4$\sqrt{2}$.
故答案为:6+4$\sqrt{2}$.
点评 本题考查基本不等式的运用,考查学生分析解决问题的能力,正确运用基本不等式是关键,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (-∞,0) | C. | (1,+∞) | D. | (-∞,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 茎叶图 | B. | 分层抽样 | C. | 独立性检验 | D. | 回归直线方程 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
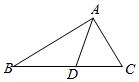 如图,在三角形ABC中,AB=2,AC=1,cos∠BAC=$\frac{1}{3}$,∠BAC的平分线交BC于点D.
如图,在三角形ABC中,AB=2,AC=1,cos∠BAC=$\frac{1}{3}$,∠BAC的平分线交BC于点D.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com